(42)王道数据结构-邻接表法

基本概念

当一个图为稀疏图时，使用邻接矩阵表示显然要浪费大量的存储空间，而图的邻接表法结合了顺序存储和链式存储方法，大大减少了这种不必要的浪费。

邻接表，是指对图G中的每一个顶点vi建立一个单链表，第 i 个单链表中的结点表示依附于顶点 vi 的边（对于有向图则是以顶点vi为尾的弧），这个单链表就称为顶点vi的边表（对于有向图则称为出边表）。边表的头指针和顶点的数据信息采用顺序存储（成为顶点表），所以在邻接表中存在两种：顶点表结点和边表结点。

顶点表结点由顶点域（data）和指向第一条邻接边的指针（firstarc）构成，边表（邻接表）结点由邻接点域（adjvex）和指向下一条邻接边的指针域（nextarc）构成。

无向图

图的邻接表表示方式不唯一

表示法一

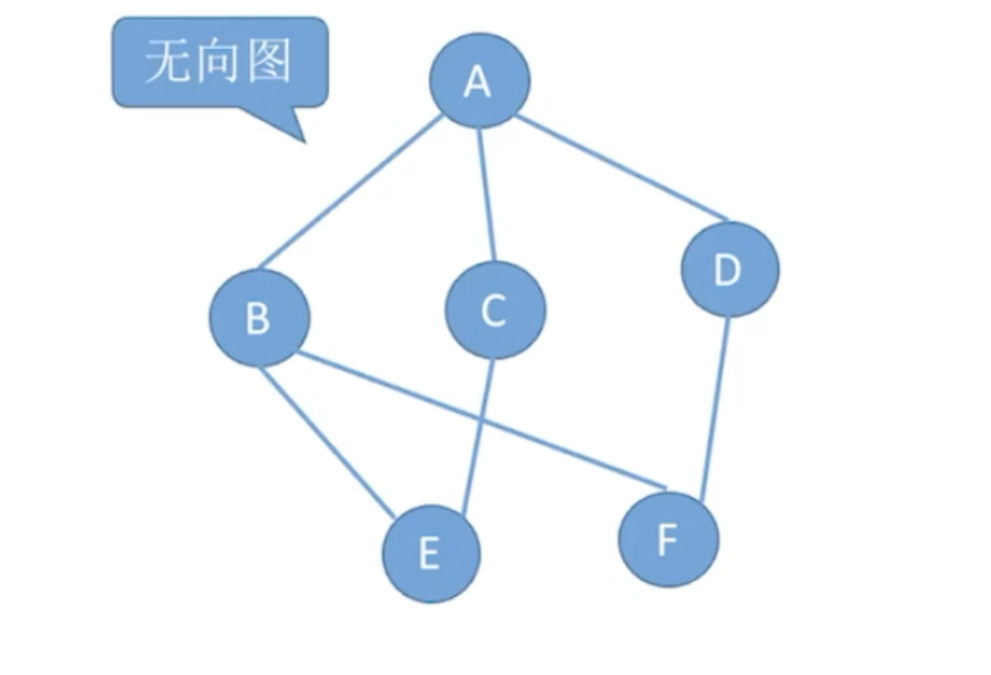
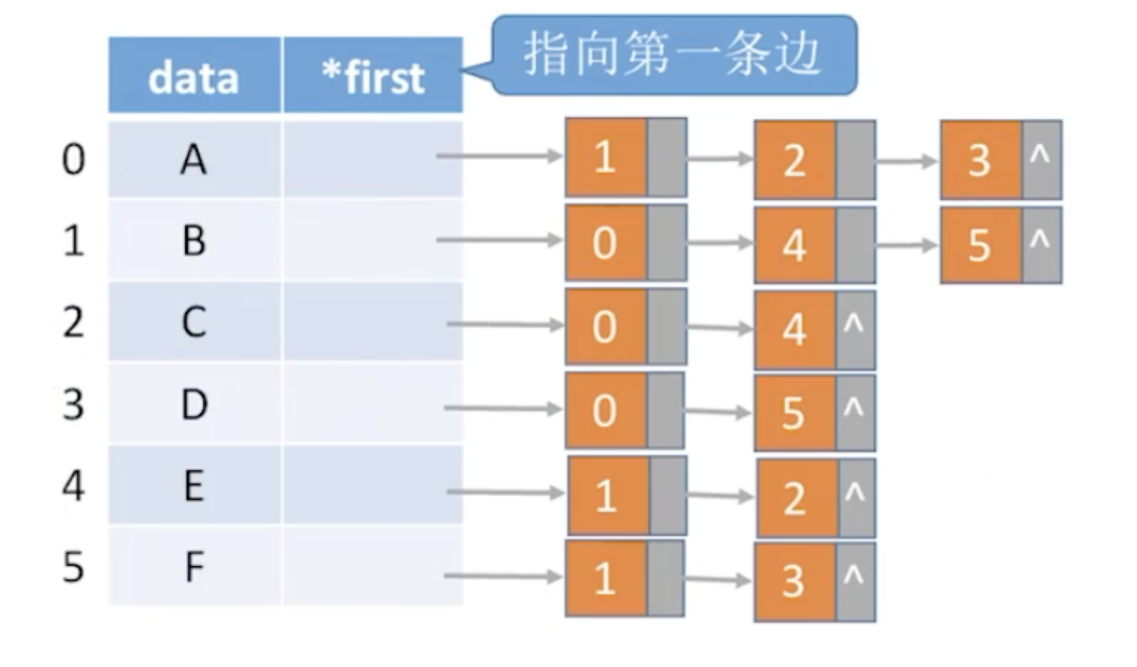
边结点的数量是2|E|,整体空间复杂度为O(|V| + 2|E|)

表示法二

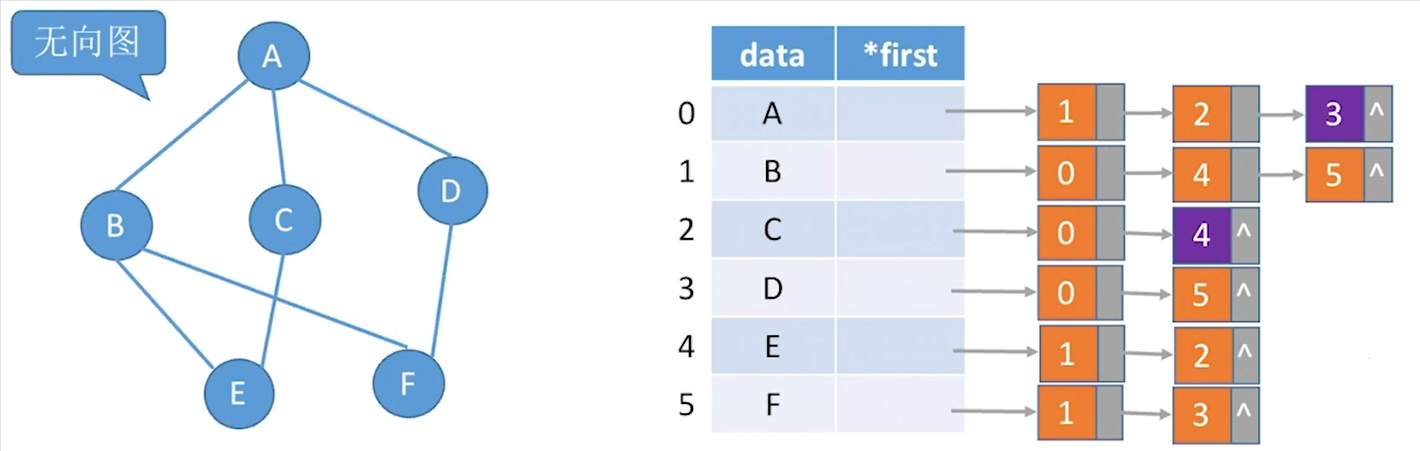
有向图

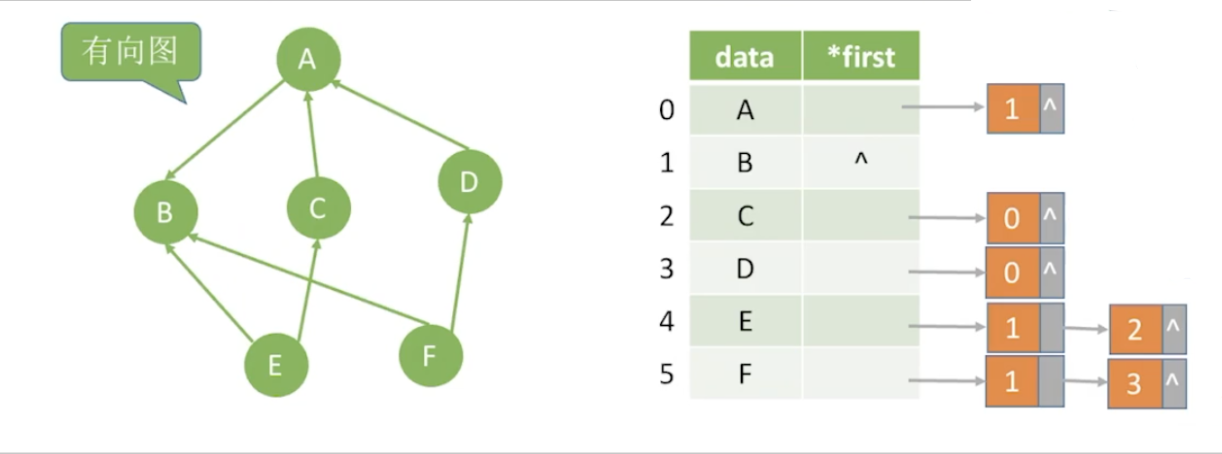
边结点的数量是|E|，整体空间复杂度为O(|V| + |E|)

表示法二

代码结构

#define MaxVertexNum 100; //图中顶点数目的最大值
//"边/弧"
typedef struct ArcNode{
    int adjvex; //边/弧指向哪个结点
    struct ArcNode *next; //指向下一条弧的指针
    //InfoType info; //边权值
}ArcNode;
//"顶点"
typedef struct VNode{
    VertexType data; //顶点信息
    ArcNode *first; //第一条边/弧
}VNode, AdjList[MaxVertexNum];
//用邻接表存储的图
typedef struct{
    AdjList vertices; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
}ALGraph; //ALGraph是以邻接表存储图类型

邻接表和邻接矩阵对比

	邻接表	邻接矩阵
空间复杂度	无向图O(|V|+2|E|);有向图O(|V| + |E|)	O(|V|^2)
适合用于	存储稀疏图	存储稠密图
表示方式	不唯一	唯一
计算度/出度/入度	计算有向图的度、入度不方便、其余很方便	必须遍历对应的行或列
找相邻的边	找有向图的入边不方便、其余很方便	必须遍历对应行或列