(41)王道数据结构-邻接矩阵法

基本概念

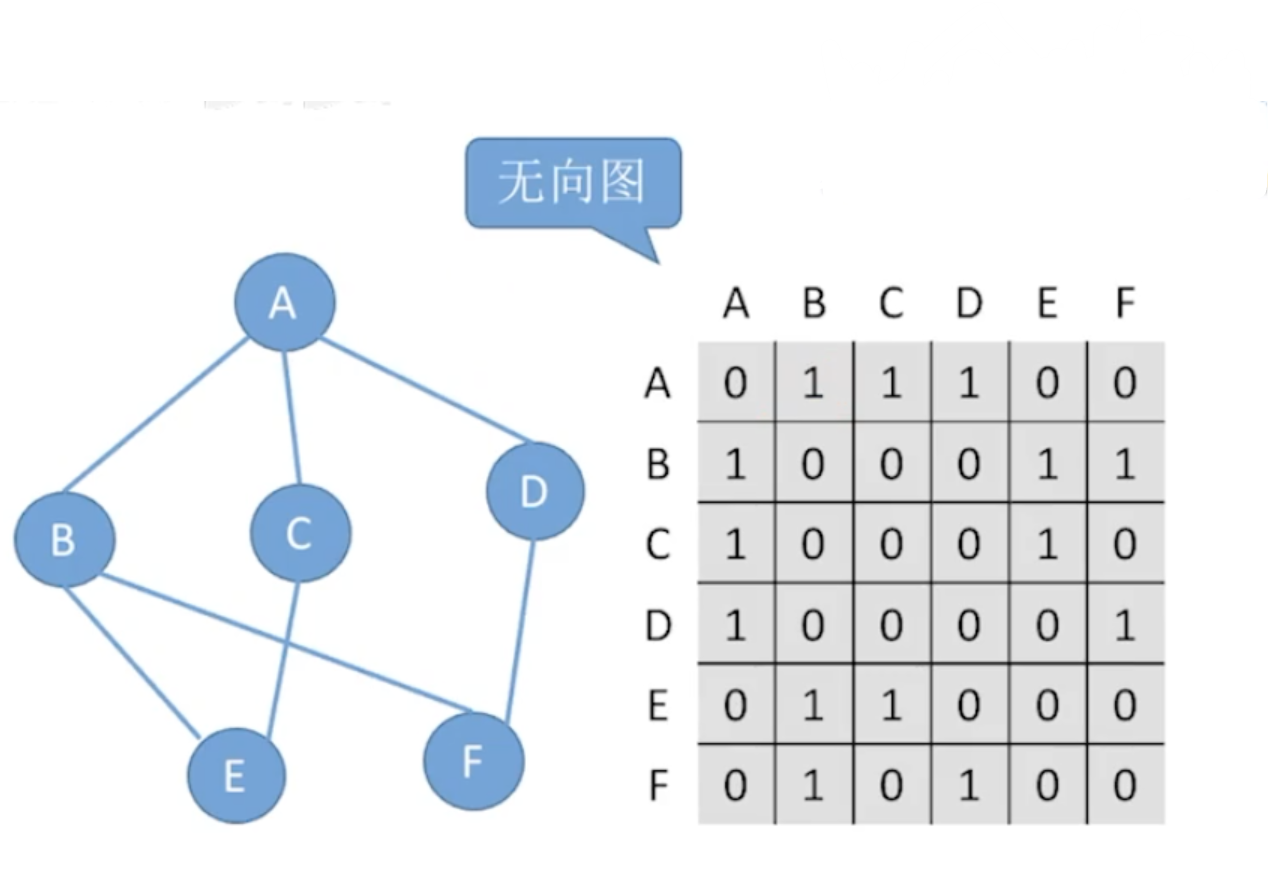
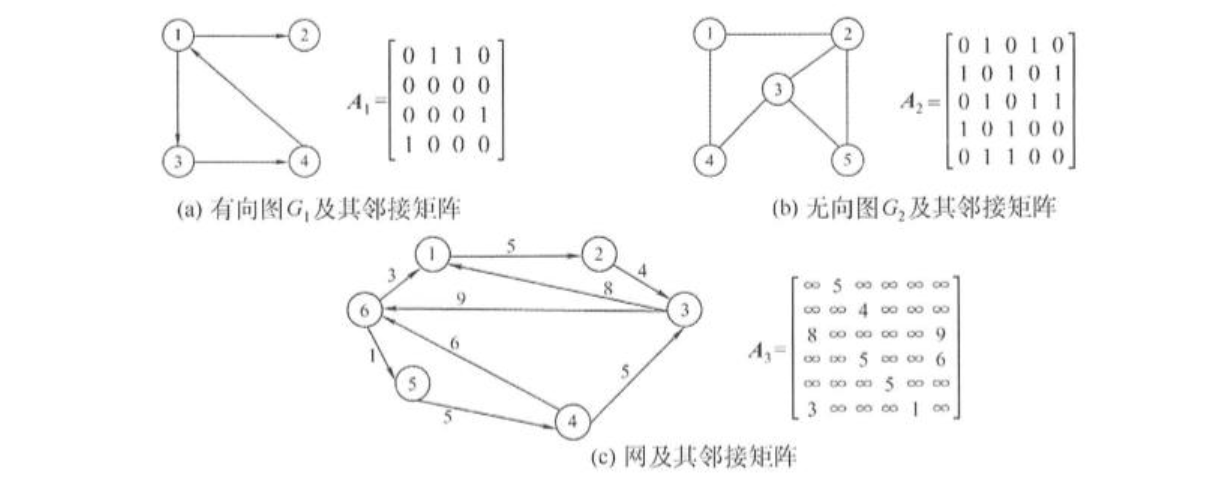
指用一个一维数组存储图中顶点的信息，用一个二维数组存储图中边的信息（即各顶点之间的邻接关系），存储顶点之间邻接关系的二维数组称为邻接矩阵。其中有指向关系用1表示，没有指向关系用0表示

结点数为n的图G=(V, E)的邻接矩阵A是nxn的。将G的顶点编号为v1, v2,…, vn。

$A[i][j]=\left\{ \begin{aligned} 1, & 若(v_i,v_j)或<v_i,v_j>是E(G)的边\\ 0, & 若(v_i,v_j)或<v_i,v_j>不是E(G)的边\\ \end{aligned} \right .$

无向图

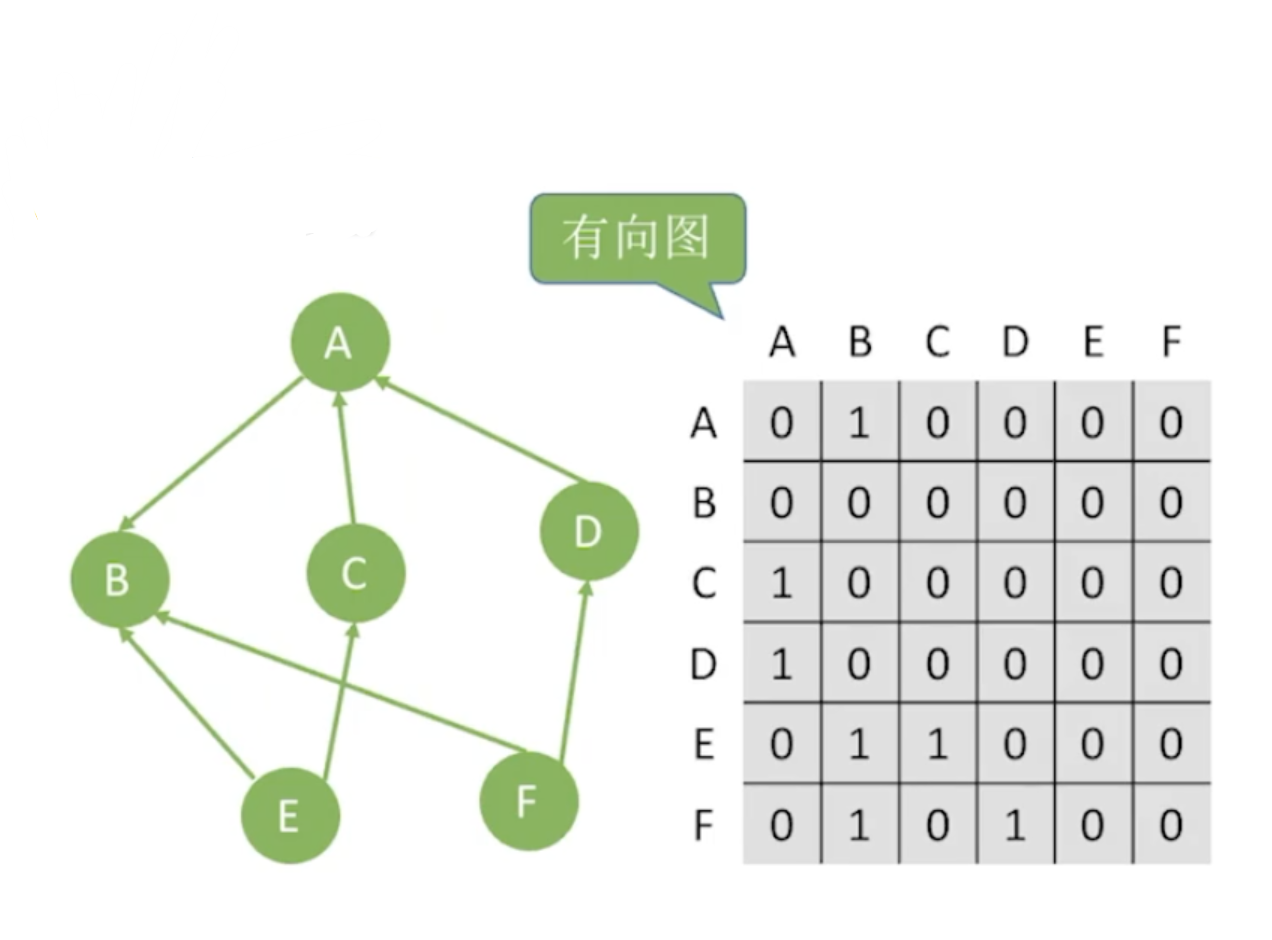
有向图

存储代码

#define MaxVertexNum 100 //顶点数目的最大值
typedef struct {
    char Vex[MaxVertexNum]; //顶点表
    int Edge[MaxVertexNum][MaxVertexNum]; //领接矩阵，边表
    int vexnum, arcnum; //图的当前顶点数和弧数
}MGraph;

1.顶点中可以存更复杂的信息
2.可以用布尔型或枚举类型变量表示边

顶点的度

第i个结点的度 = 第i行(或第i列)的非零元素个数

第i个结点的出度 = 第i行的非零元素个数

第i个结点的入度 = 第i列的非零元素个数

第i个结点的度 = 第i行、第i列的非零元素个数之和

时间复杂度

邻接矩阵法求顶点的度/出度/入度的时间复杂度为O(|V|)

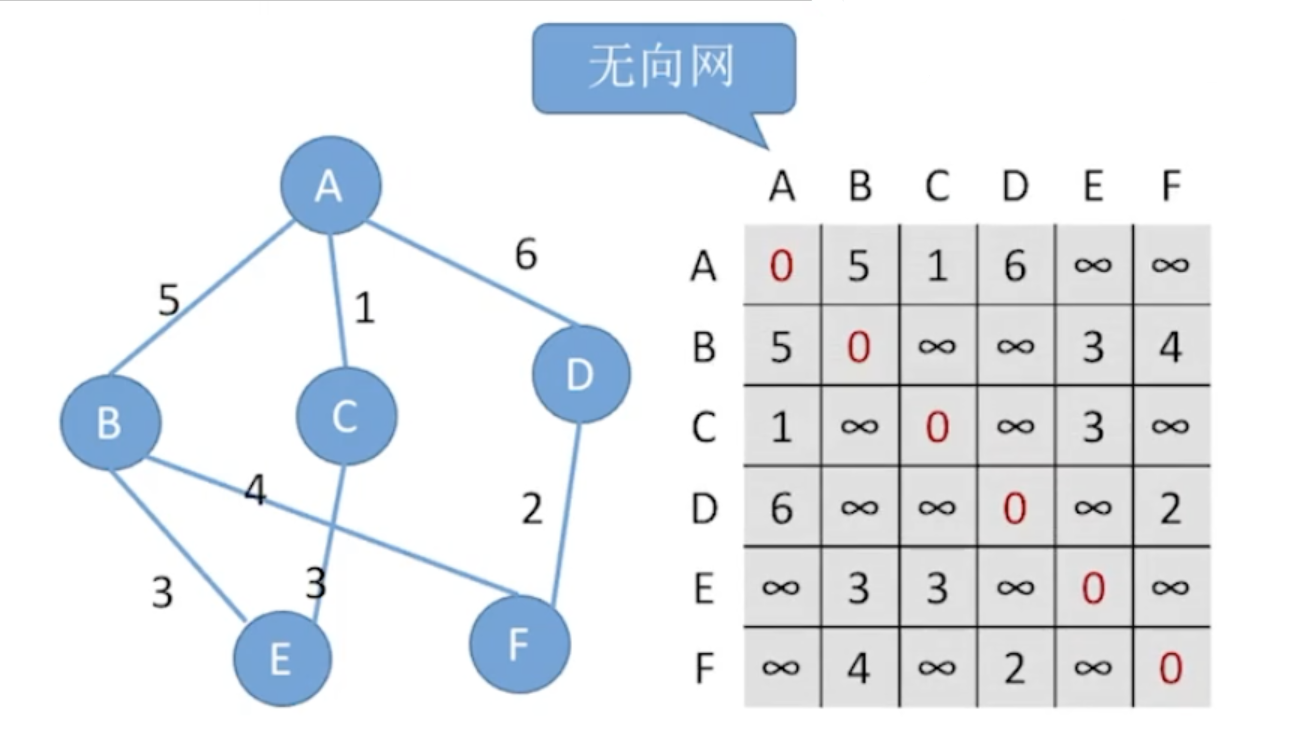
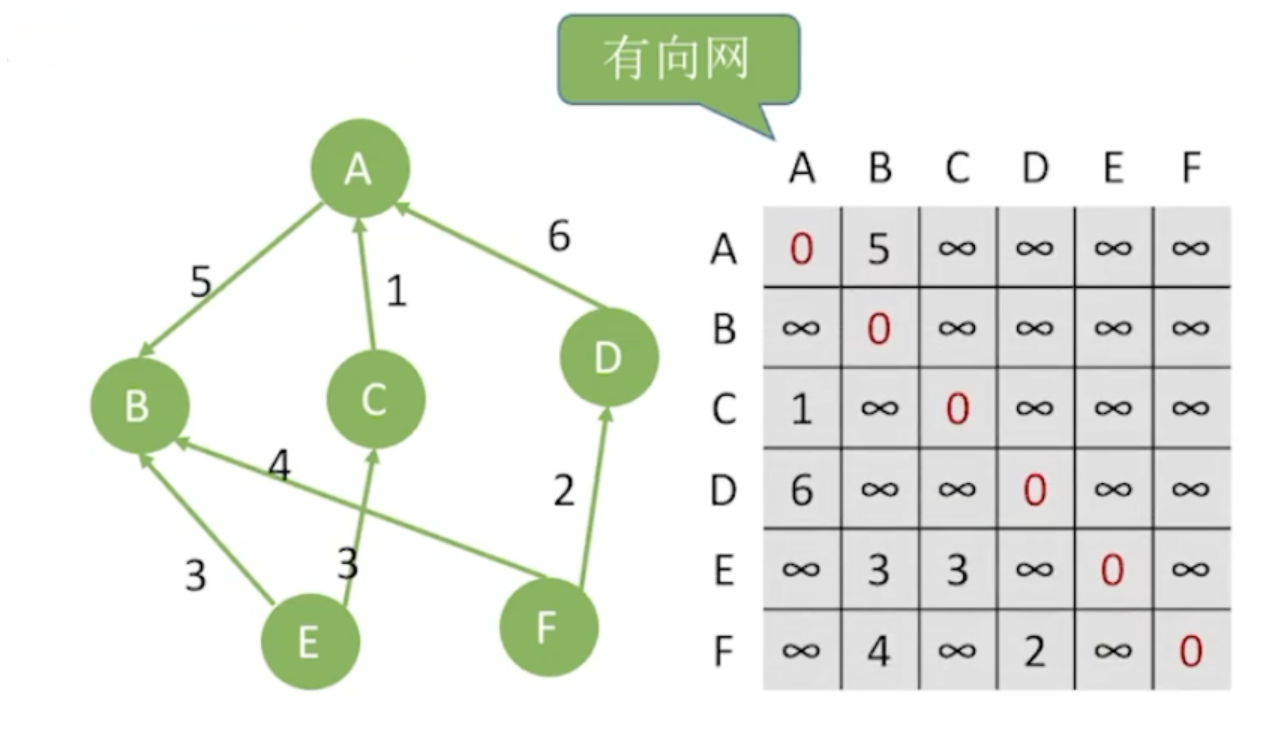
带权图(网)

代码结构

#define MaxVertexNum 100 //顶点数目的最大值
#define INFINITY 最大的int值 //宏定义常量"无穷"
typedef char VertexType; //顶点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
typedef struct {
    VertexType Vex[MaxVertexNum]; //顶点表
    EdgeType Edge[MaxVertexNum][MaxVertexNum]; //领接矩阵，边表
    int vexnum, arcnum; //图的当前顶点数和弧数
}MGraph;

无穷表示两个顶点之间不存在边(零也是相同含义)

如果G是有向带权图，则

$A[i][j]=\left\{ \begin{aligned} w_{ij} & \quad 若V_i \neq V_j且<V_i, V_j > ∈ E(G)\\ 0或∞ &\quad 其他\\ \end{aligned} \right .$

表示为

$A[i][j]=\left\{ \begin{aligned} w_{ij} & \quad 若V_i \neq V_j且<V_i, V_j > ∈ E(G)\\ 0 &\quad 若V_i = V_j \\ ∞ & \quad 若<V_i,V_j> ∉E(G) \end{aligned} \right .$

无向网

有向网

性能分析

①在简单应用中，可直接用二维数组作为图的邻接矩阵（顶点信息等均可省略）。
②当邻接矩阵中的元素仅表示相应的边是否存在时，EdgeType可定义为值为0和1的枚举类型。
③无向图的邻接矩阵是对称矩阵，对规模特大的邻接矩阵可采用压缩存储。
④邻接矩阵表示法的空间复杂度为O(n2)，其中n为图的顶点数|V|。

重要性质

1.空间复杂度O(|V|^2)只和顶点数相关，和实际的边数无关
2.适合用于存储稠密图
3.无向图的邻接矩阵是对称矩阵，可以压缩存储(只存储上三角区/下三角区)

常用性质

①无向图的邻接矩阵一定是一个对称矩阵（并且唯一）。因此，在实际存储邻接矩阵时只需存储上（或下）三角矩阵的元素。
②对于无向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数正好是第i个顶点的度TD(vi)。
③对于有向图，邻接矩阵的第i行（或第i列）非零元素（或非∞元素）的个数正好是第i个顶点的出度OD(vi)（或入度ID(vi)）。
④用邻接矩阵法存储图，很容易确定图中任意两个顶点之间是否有边相连。但是，要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。这是用邻接矩阵存储图的局限性。
⑤稠密图适合使用邻接矩阵的存储表示。

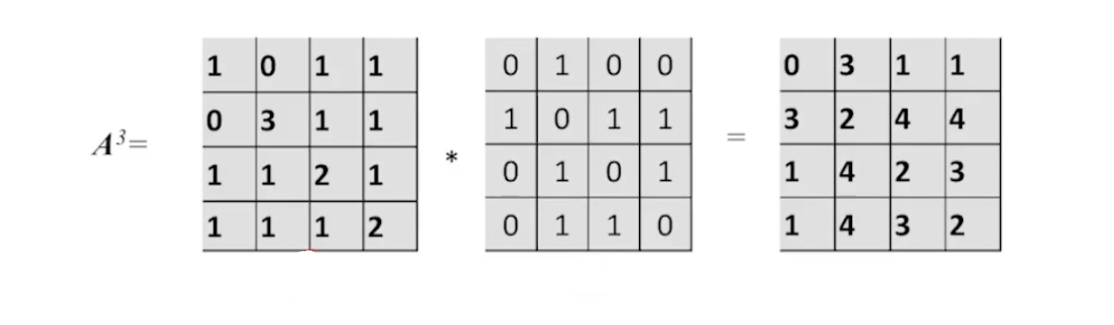
示例一

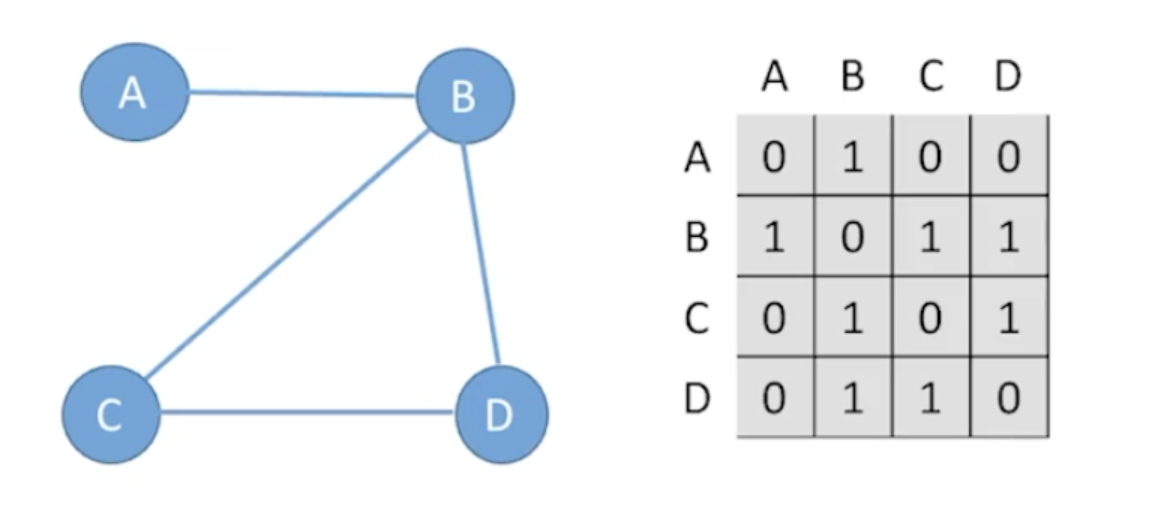
设图G的邻接矩阵为A(矩阵元素为0/1)，则A^n的元素A^n[i][j]等于由顶点i到顶点j的长度为n的路径的数目

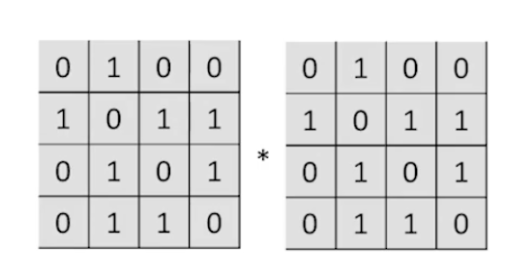
$\begin{aligned} A^2[1][4] = a_{1,1}a_{1,4} + a_{1,2}a_{2,4} + a_{1,3}a_{3,4} + a_{1,4}a_{4,4} = 1 \\ A^2[2][2] = a_{2,1}a_{1,2} + a_{2,2}a_{2,2} + a_{2,3}a_{3,2} + a_{2,4}a_{4,2} = 3 \\ A^2[3][3] = a_{3,1}a_{1,3} + a_{3,2}a_{2,3} + a_{3,3}a_{3,3} + a_{3,4}a_{4,3} = 1 \\ A^2[1][2] = a_{1,1}a_{1,2} + a_{1,2}a_{2,2} + a_{1,3}a_{3,2} + a_{1,4}a_{4,2} = 0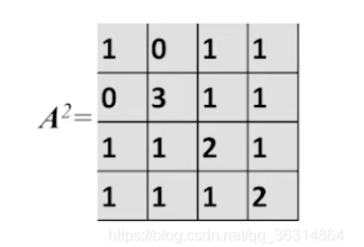 \\ \end{aligned}$

示例二

设图G的邻接矩阵为A(矩阵元素为0/1)，则A^n的元素A^n[i][j]等于由顶点i到顶点j的长度为n的路径的数目