(52)王道数据结构-拓扑排序

原文地址:拓扑排序

基本概念

拓扑排序（Topological Order）是指，将一个有向无环图（Directed Acyclic Graph）进行排序进而得到一个有序的线性序列

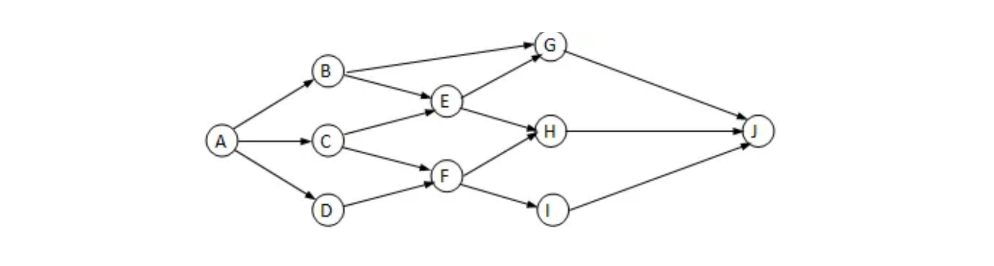
可能存在的拓扑排序:

1.A,B,C,D,E,F,G,H,I,J

2.A,C,D,B,E,F,G,H,I,J

3.A,D,C,B,E,F,G,H,I,J

4.A,B,D,C,E,F,G,H,I,J

操作步骤

我们还是利用队列来完成，我们每次只需要将那些入度为0的顶点，丢进队列中（注意丢进去之后记得更新一下图中其他顶点的入度）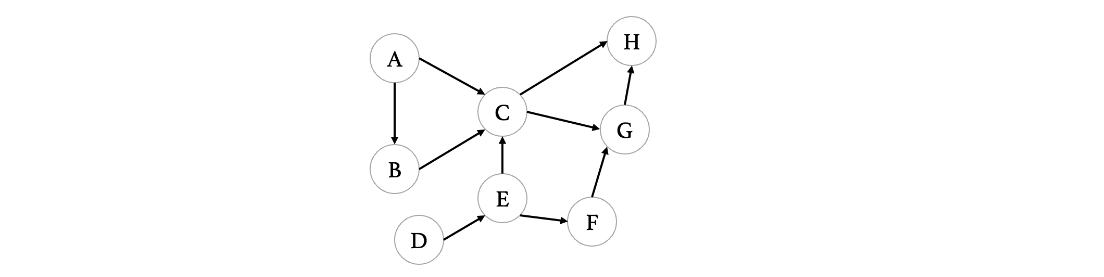

第一次操作

队列中有A是入度为0的顶点
队列:A

第二次操作

队列中除了A以外还有D是入度为0的顶点
队列:A,D

当目前所有度数为0的顶点进入队列之后，我们开始出队，正式开始拓扑排序，在出队时直接打印，并且查看，当此顶点离开图之后，图中会不会有其他顶点的入度变为0，如果有，将其他顶点入队

第三次操作

因为目前所有入度为零的顶点已经全部加入队列，所以需要A出队。出队之后A不和其他顶点关联，加入到排序的序列。A出队之后B变成了入队为0的顶点
队列:D,B
排序:A

第四次操作

和之前的操作同理，这次是D出队。这时候队列中E为入队为0的顶点
队列: B, E
排序: A, D

第五次操作

和之前的操作同理，这次是B出队。这时候队列中E为入队为0的顶点。此时无任何入度为0的顶点，只需要继续将E出队
队列: E
排序: A, D, B

第六次操作

E出队之后出现了C和F为入度为0的顶点，统统入队
队列: C, F
排序: A, D, B, E

第七次操作

继续将C出队，我们发现没有任何顶点入队变为0，我们继续来看F
队列: F
排序: A, D, B, E, C

第八次操作

当F出队后，顶点G变成了入度为0的顶点，此时将G入队
队列: G
排序: A, D, B, E, C, F

最后操作

经过如上操作最后得到了拓扑排序
拓扑排序: A, D, B, E, C, F