(40)王道数据结构-哈夫曼树

基本概念

路径: 定点Vp到顶点Vq之间的一条路径是指顶点序列，有向图的路径也是有向的。无向图之间可能不存在路径
$$
V_p，V_{i_1}，V_{i_2}，…，V_{i_m}，V_q
$$

回路: 第一个顶点和最后一个顶点相同的路径称为回路或环

简单路径: 在路径序列中，顶点不重复出现的路径称为简单路径

路径长度: 路径上边的数目

点到点的距离 从顶点u出发到顶点v的最短路径若存在，则此路径长度称为从u到v的距离。若从u到v根本不存在路径，则记该距离为无穷(∞)

连通: 无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的

强连通: 若从顶点v到顶点w和从顶点w到顶点v之间都有路径，则称这两个顶点是强连通的

常见的图

连通图

若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图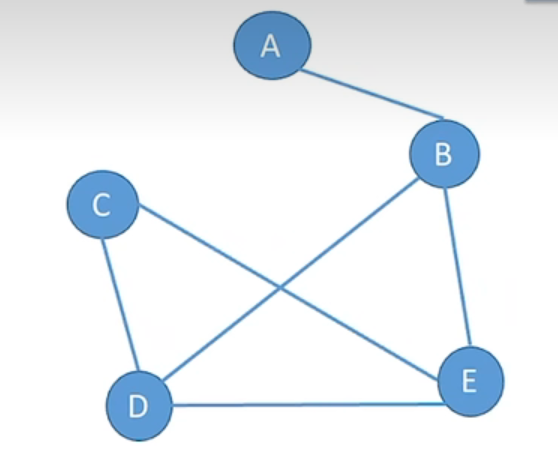

考点:
对于n个顶点的无向图G
1.若G是连通图，则最少有n-1条边
2.若G是非连通图，则最多可能有
$$
C_{n-1}^2
$$
条边

强连通图

若图中任何一对顶点都是强连通的，则称此图为强连通图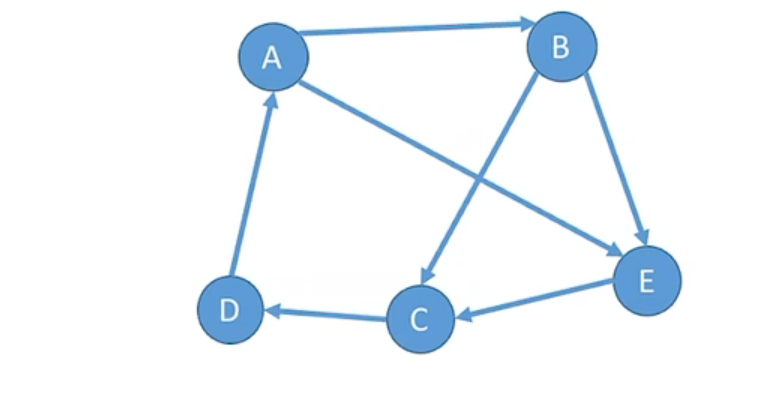

考点:
对于n个顶点的有向图G
1.若G是强连通图，则最少有n条边(形成回路)

子图

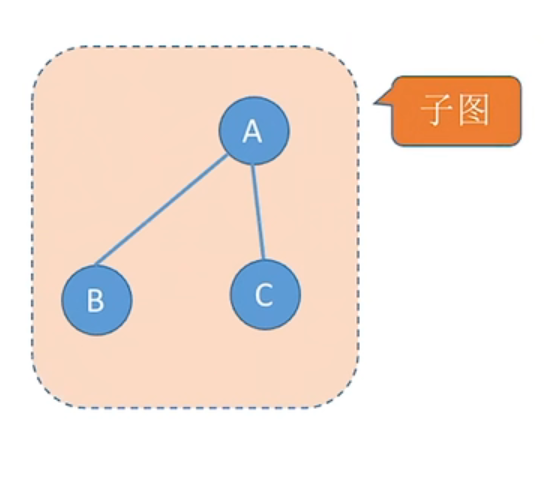
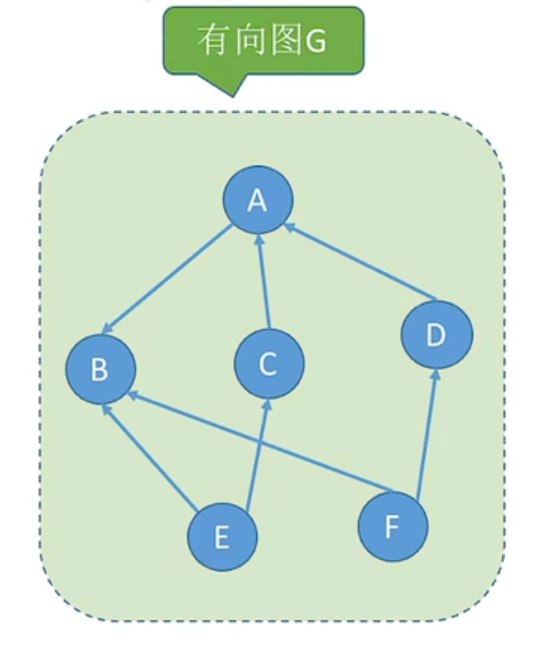
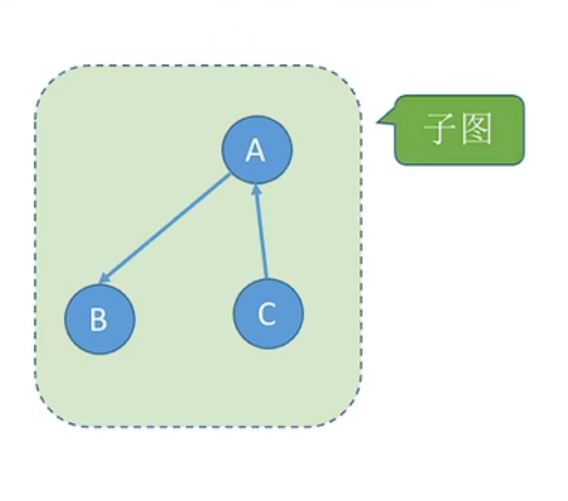
设有两个图G=(V,E)和G′=(V′,E′),若V′是V的子集，且E′是E的子集，则称G′是G的子图

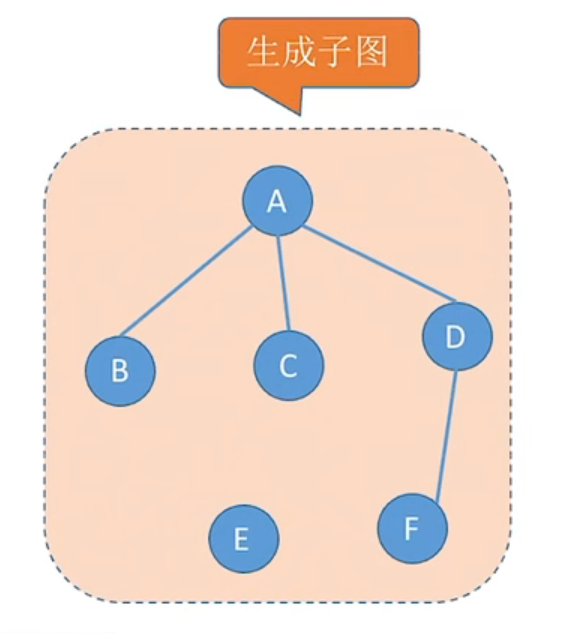
若满足V(G′)=V(G)的子图G′，则称其为G的生成子图。并非任意挑选几个点、几条边都能构成子图

无向图

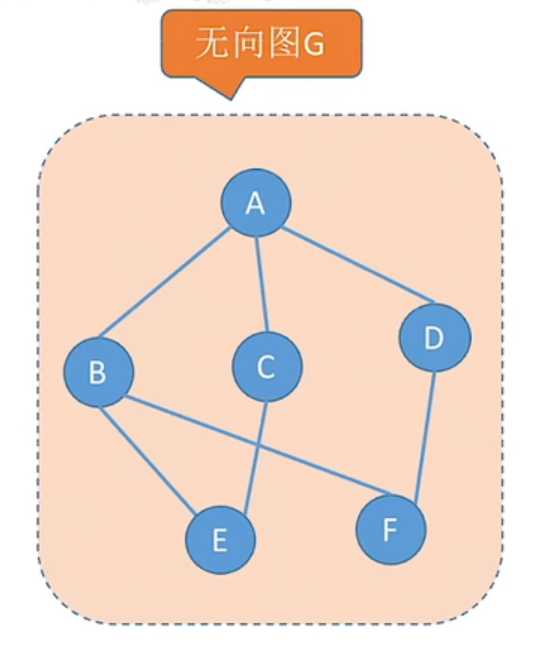
连通分量:
无向图中极大连通子图称为连通分量，子图必须连通，且包含尽可能多的顶点和边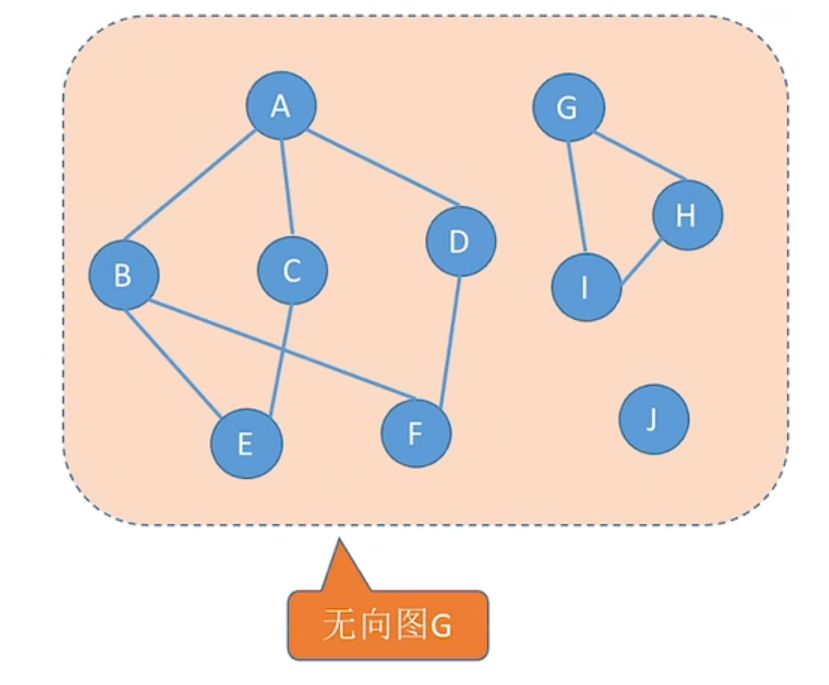

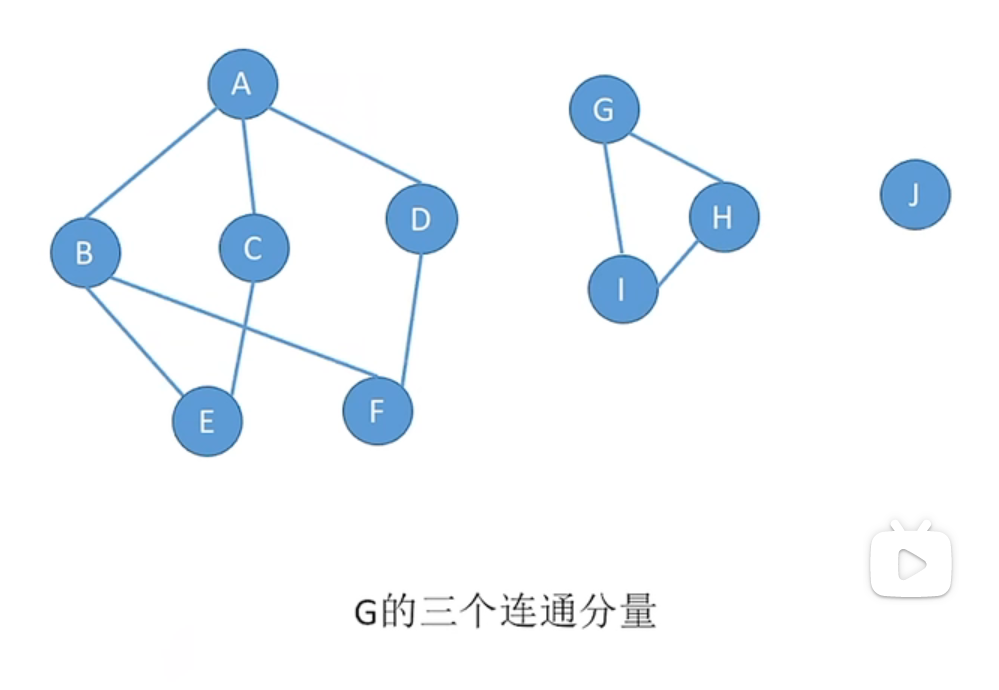
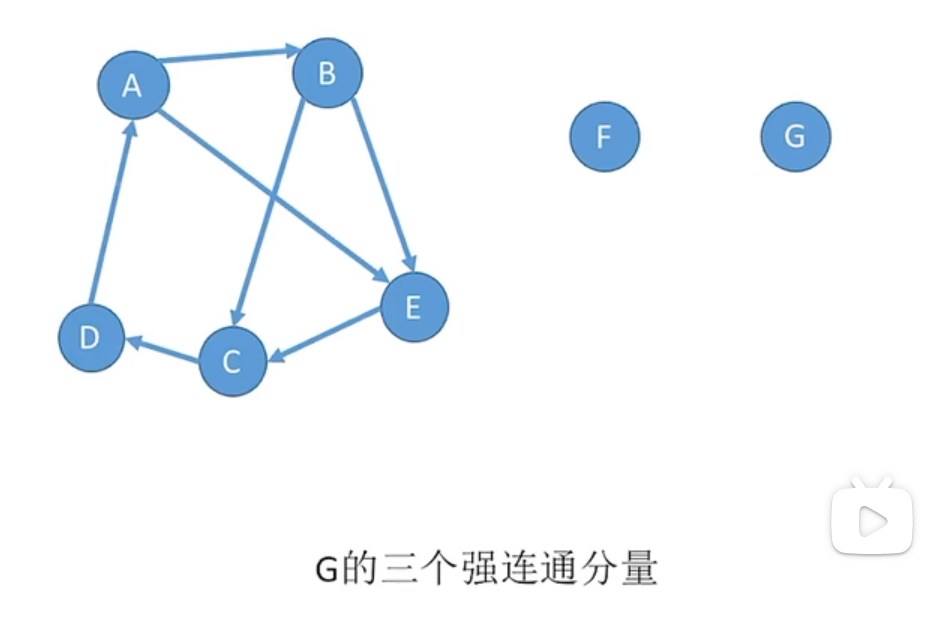
强连通分量:
有向图中的极大强连通子图称为有向图的强连通分量，子图必须强连通，同时保留尽可能多的边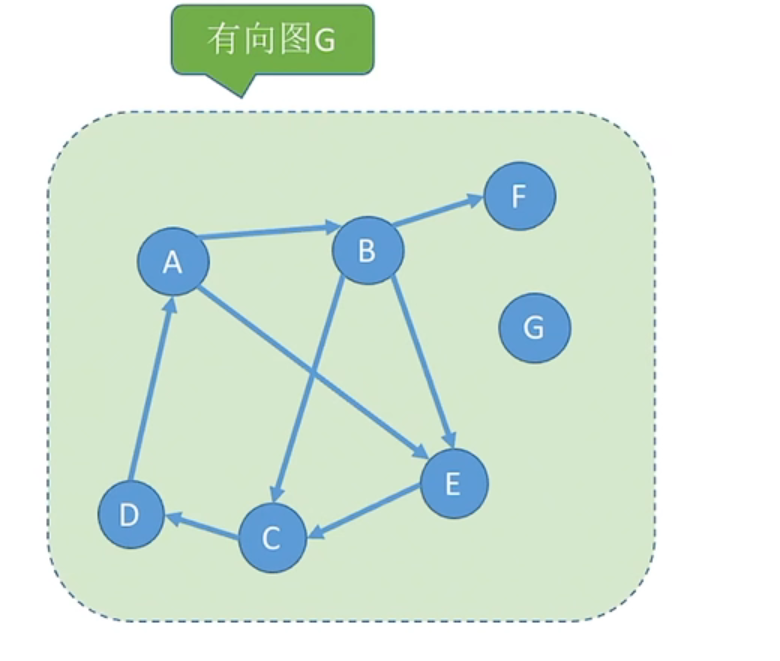

有向图

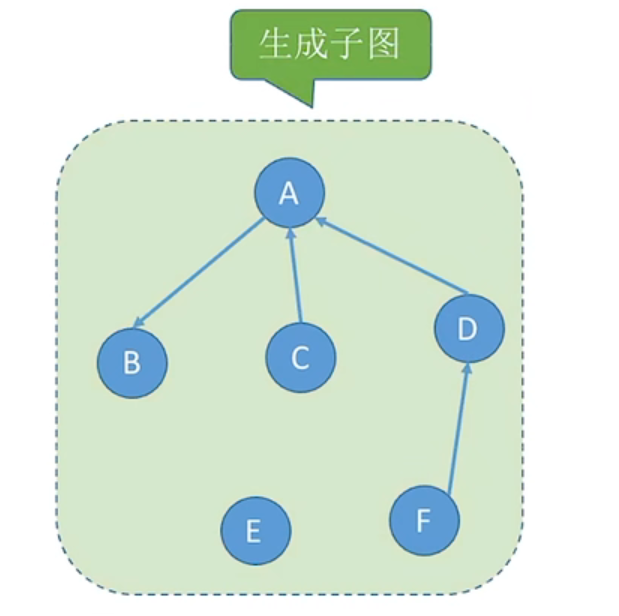
生成树

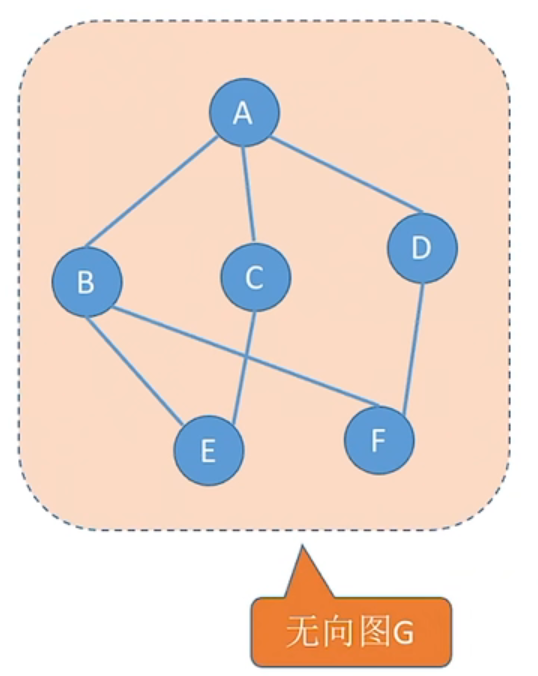
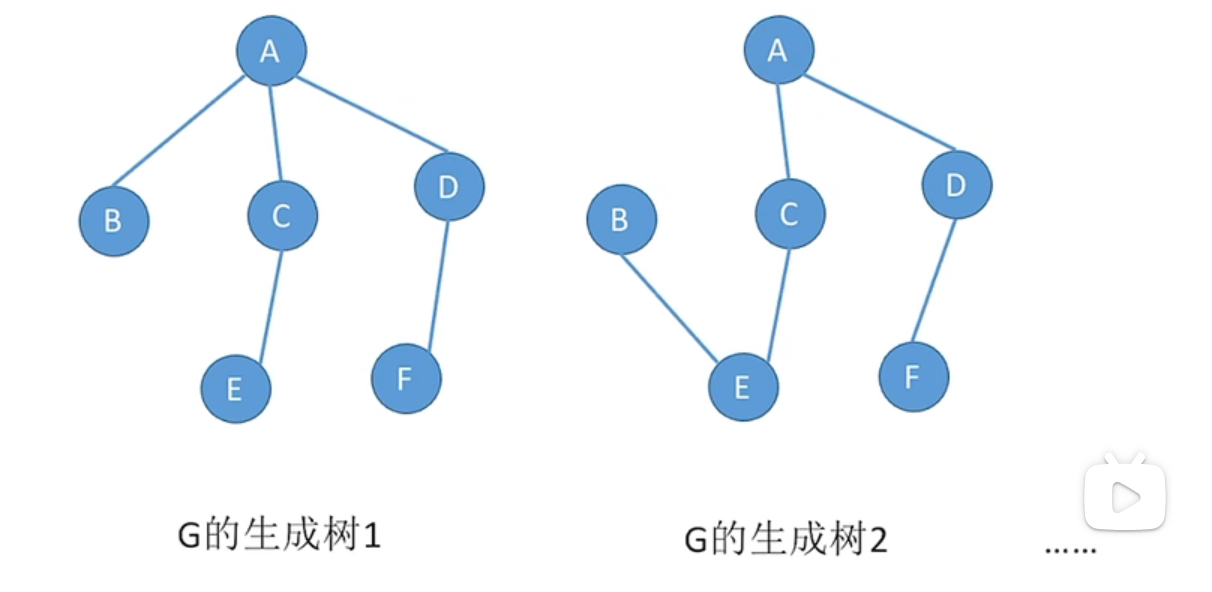
连通图的生成树是包含图中全部顶点的一个极小连通子图。边尽可能的少，但要保持连通

若图中顶点树为n，则它的生成树含有n-1条边。对于生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边会形成一个回路

重要概念

实际距离: 给各边赋予一个权值

转发概率: 给各边赋予一个数值

边的权: 在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值

带权网/图: 边上带有权值的图称为带权图，也称网

带权路径长度: 当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

特殊的图

无向完全图

无向图中任意两个顶点之间都存在边，若无向图的顶点数|V|=n,则
$$
|E|∈[0,C_n^2] = [0, \frac{n(n-1)}{2}]
$$

有向完全图

在有向图中任意两个顶点之间都存在方向相反的两条弧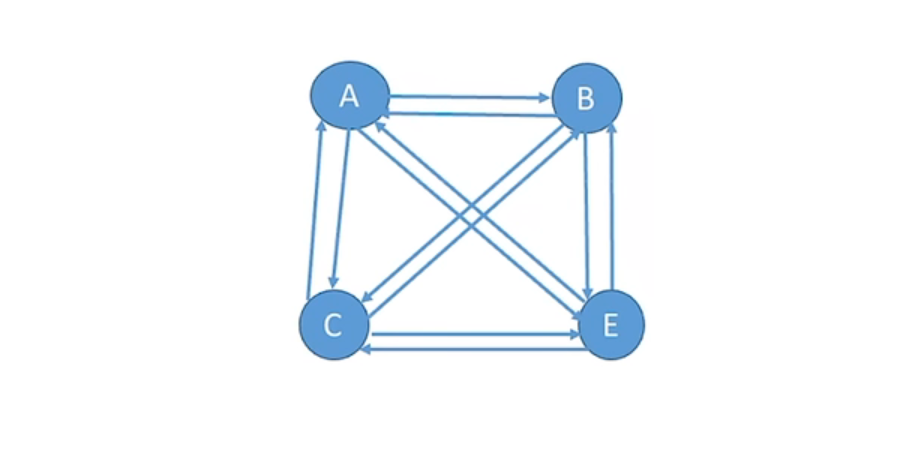

稀疏图/稠密图

边数很少的图称为稀疏图，没有一个绝对的界限，一般来讲|E| < |V|log|V|时,可以将G视为稀疏图

树

不存在回路，且连通的无向图。

1.n个顶点的树,必有n-1条边
2.n个顶点的图，若|E| > n - 1，则一定有回路

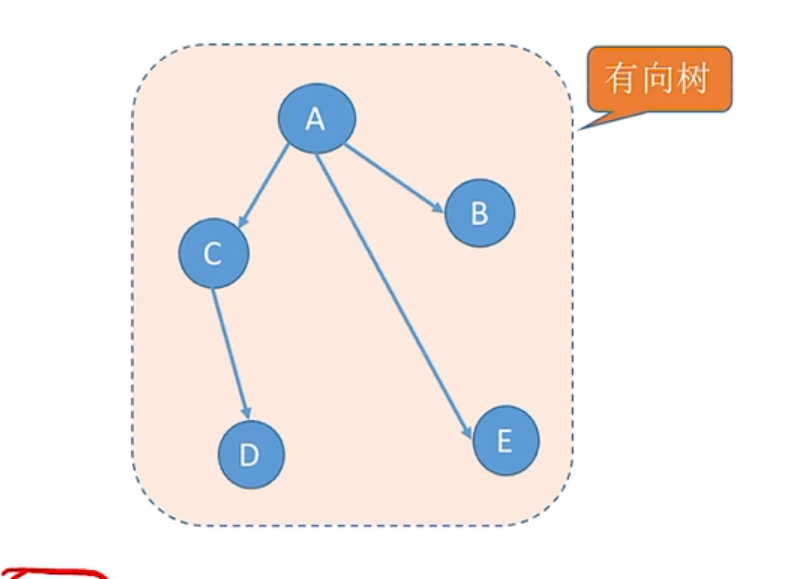
有向树

一个顶点的入度为0、其余顶点的入度均为1的有向图，称为有向树