(50)王道数据结构-最短路径问题(Floyd)

原文地址:Floyd

基本概念

是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权（但不可存在负权回路）的最短路径问题，同时也被用于计算有向图的传递闭包

基本规则

1.从1开始，一直到n（n就是顶点数）的一个矩阵序列A1、A2、…An，我们需要从最初的邻接矩阵开始，从A1开始不断往后推

2.每一轮，我们都会去更新那些非对角线（对角线都是0，更新了还是0，所以说没必要看）、i行i列以外的元素，判断水平和垂直方向投影的两个元素之和是否比原值小，如果是，那就更新为新的值。迭代公式为：
$$
A_k(i,j) = min(A_{k-1}(i,j), A_{k-1}(i,k) + A_{k-1}(k,j))
$$

3.经历n轮后，最后得到的就是最终的最短距离了。

操作步骤

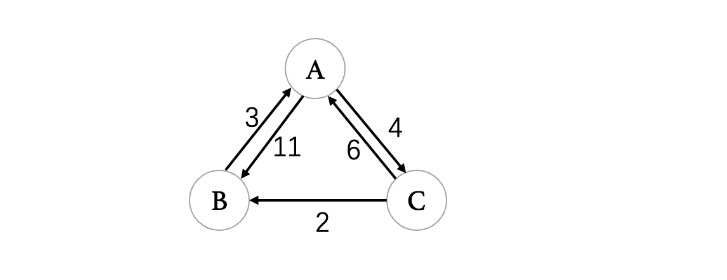
需要注意的是权值不能出现负数，否则会出现问题

邻接矩阵

	A	B	C
A	0	11	4
B	3	0	∞
C	6	2	0

第一轮

从第一轮开始，第一轮是基于原有的邻接矩阵来进行处理的:

	A	B	C
A	0	11	4
B	3	0	∞
C	6	2	0

matrix[行][列] = matrix[行][论数] + matrix[轮数][列]

1.除了对角线元素之外，还有matrix[0][1], matrix[0][2], matrix[1][0],matrix[1][2],matrix[2][0],matrix[2][1]
(下标从0开始，第一轮用0表示)

2.各个元素分析
第一个元素:
matrix[0][1] = min{ matrix[0][0] + matrix[0][1], matrix[0][1]}
matrix[0][1] = min{11, 11} (相同则不变)

第二个元素:
matrix[0][2] = min{ matrix[0][0] + matrix[0][2], matrix[0][2]}
matrix[0][1] = min{4, 4} (相同则不变)

第三个元素:
matrix[1][0] = min{ matrix[1][0] + matrix[0][0], matrix[1][0]}
matrix[1][0] = min{3, 3} (相同则不变)

第四个元素:
matrix[1][2] = min{ matrix[1][0] + matrix[0][2], matrix[1][2]}
matrix[1][2] = min{3 + 4, ∞} (小于变为7)

第五个元素:
matrix[2][0] = min{ matrix[2][0] + matrix[0][0], matrix[2][0]}
matrix[2][0] = min{6, 6} (相同则不变)

第六个元素:
matrix[2][1] = min{ matrix[2][0] + matrix[0][1], matrix[2][1]}
matrix[2][0] = min{6 + 11, 6} (大于则不变)

最终结果:

	A	B	C
A	0	11	4
B	3	0	7
C	6	2	0

第二轮

第二轮操作步骤和第一轮同理

	A	B	C
A	0	11	4
B	3	0	7
C	5	2	0

第三轮(最后一轮)

第三轮操作步骤和第一轮同理

	A	B	C
A	0	6	4
B	3	0	7
C	5	2	0

实现代码

操作的图

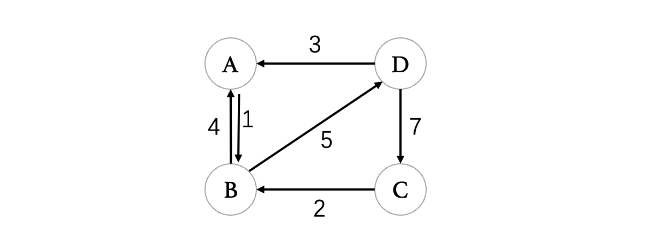
邻接矩阵

	A	B	C	D
A	0	1	∞	∞
B	4	0	∞	5
C	∞	2	0	∞
D	3	∞	7	0

完整代码

#define INF 210000000
#define N 4
int min(int a, int b) {
    return a > b ? b : a;
}

void floyd(int matrix[N][N], int n){
    for (int k = 0; k < n; ++k) { //一共需要执行K轮
        for (int i = 0; i < n; ++i) { //i和j从0开始就行了，直接全看，不会影响结果的
             for (int j = 0; j < n; ++j) {
                 matrix[i][j] = min(matrix[i][k] + matrix[k][j], matrix[i][j]);   //按照规则更新就行了
             }
        }
    }
}

int main() {
    int matrix[N][N] = {{0, 1, INF, INF},
                        {4, 0, INF, 5},
                        {INF, 2, 0, INF},
                        {3, INF, 7, 0}};

    floyd(matrix, N);

    for (int i = 0; i < N; ++i) {
        for (int j = 0; j < N; ++j) {
            printf("%d ", matrix[i][j]);
        }
        putchar('\n');
    }
}