(45)王道数据结构-图的广度优先遍历
基本概念
广度优先搜索类似于二叉树层次遍历算法,其基本思想是:首先访问起始顶点v,接着由v出发,依存访问v的各个未访问过的邻接顶点w1,w2,…,wi,然后依次访问w1,w2,…,wi的所有未被访问过的邻接顶点;再从这些访问过的顶点出发,访问它们所有未被访问过的邻接顶点······依次类推,直到图中所有顶点都被访问过为止。Dijkstra单源最短路径算法和Prim最小生成树算法也应用了类似的思想。
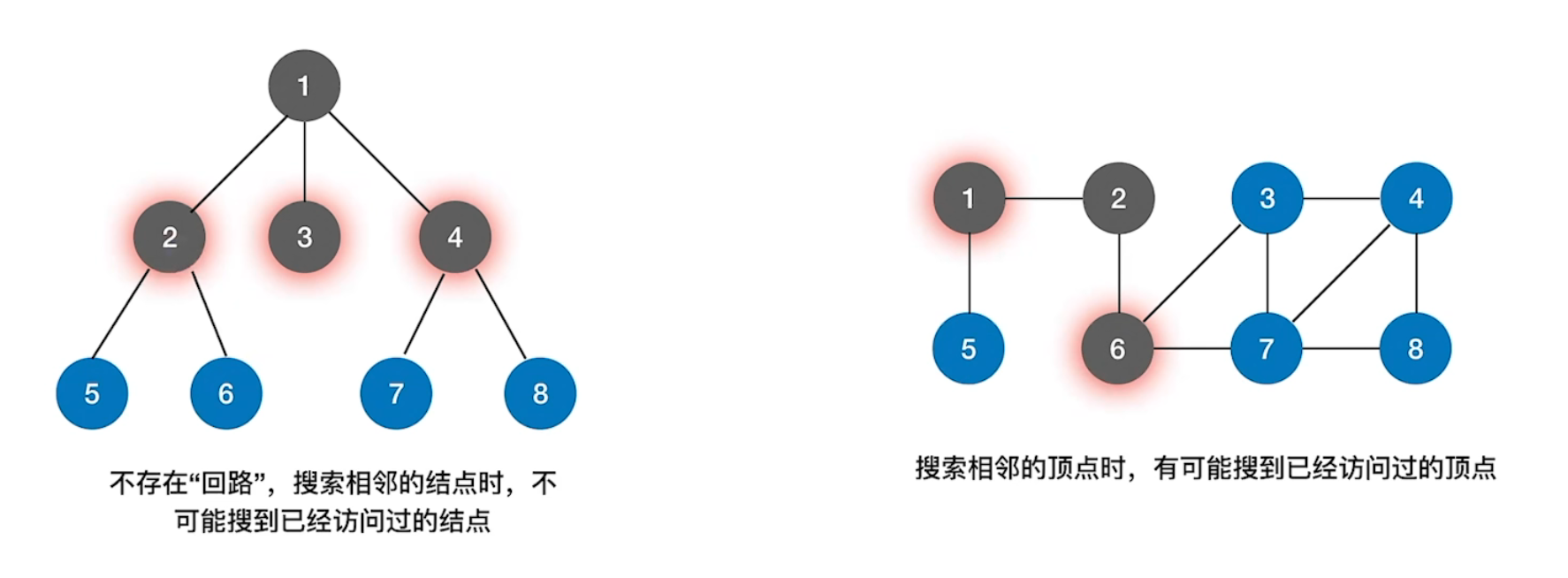
树VS图
树的广度优先遍历(层次遍历)
①若树非空,则根结点入队
②若队列非空,队头元素出队并访问,同时将该元素的孩子依次处理
③重复②直到队列非空
代码实现
广度优先搜索是一种分层的查找过程,每向前一步可能访问一批顶点,不像深层优先搜索那样有往回退的情况,因此它不是一个递归的算法。为了实现逐层的访问,算法必须借助一个辅助队列,以记忆正在访问的顶点的下一层顶点。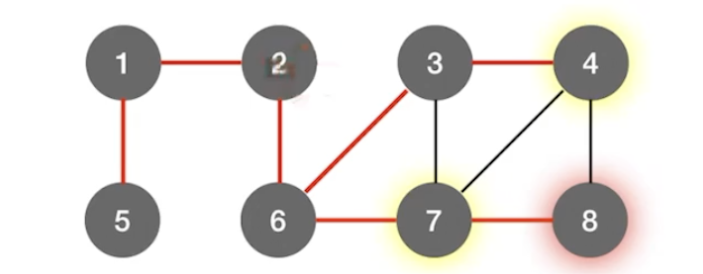

要点:
1.找到与一个顶点相邻的所有顶点
2.标记那些顶点被访问过
3.需要一个辅助队列
FirstNeighbor(G, x): 求图G中顶点x的第一个邻接点,若有则返回顶点号。若x没有邻接点或图中不存在x,则返回-1
NextNeighbor(G, x, y): 假设图G中顶点y是顶点x的一个相邻点,返回除y之外顶点x的下一个邻接点的顶点号,若y是x的最后一个邻接点,则返回-1
bool visited[MAX_VERTEX_NUM]; //访问标记数组
1 | |
本算法中如果是非连通图,则无法遍历完所有结点

遍历序列
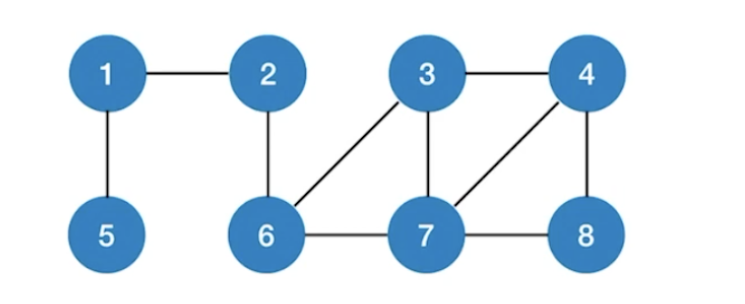
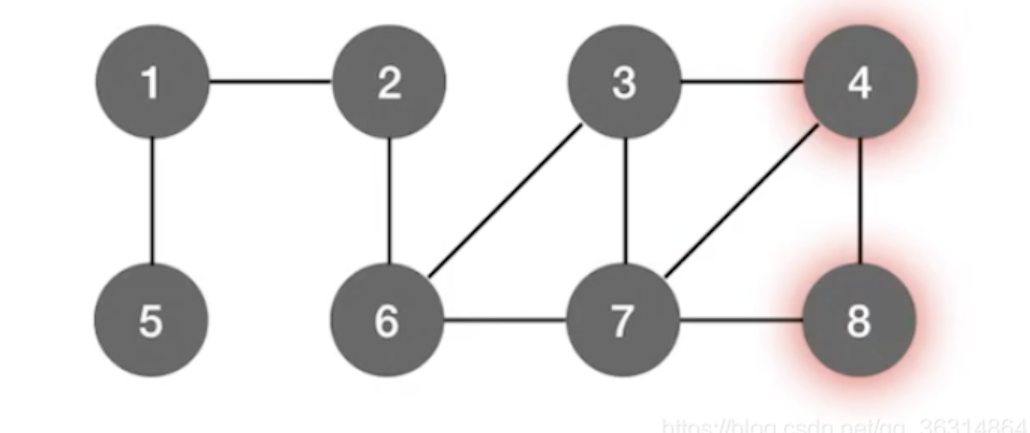
从顶点1出发得到的广度优先遍历序列:
1,2,5,6,3,7,4,8
从顶点3出发得到的广度优先遍历序列:
3,4,6,7,8,2,1,5
从顶点2出发得到的广度优先遍历序列
2,1,6,5,3,7,4,8
可变性
1.同一个图的邻接矩阵表示方式唯一,因此广度优先遍历序列唯一
2.同一个图邻接表表示方法不唯一,因此广度优先遍历序列不唯一
BFS(最终版)
对于无向图,调用BFS函数的次数=连通分量数
1 | |

辅助数组visited[]标志顶点是否被访问过,其初始状态为FALSE。在图的遍历过程中,一旦某个顶点vi被访问,就立即置visited[i]为TRUE,防止它被多次访问。
复杂度分析
空间复杂度
无论是邻接表还是邻接矩阵的存储方式,BFS算法都需要借助一个辅助队列Q,n个顶点均需要入队依次,在最坏的情况下,空间复杂度为O(|V|)。
时间复杂度
1.采用邻接表存储方式时,每个顶点均需要搜索一次(或入队一次),故时间复杂度为O(|V|),在搜索任一顶点的邻接点时,每条边至少访问一次,故时间复杂度为O(|E|),算法总的时间复杂度为O(|V|+|E|)
2.采用邻接矩阵存储方式时,查找每个顶点的邻接点所需的时间为O(|V|),故算法的时间复杂度为O(|V|2)
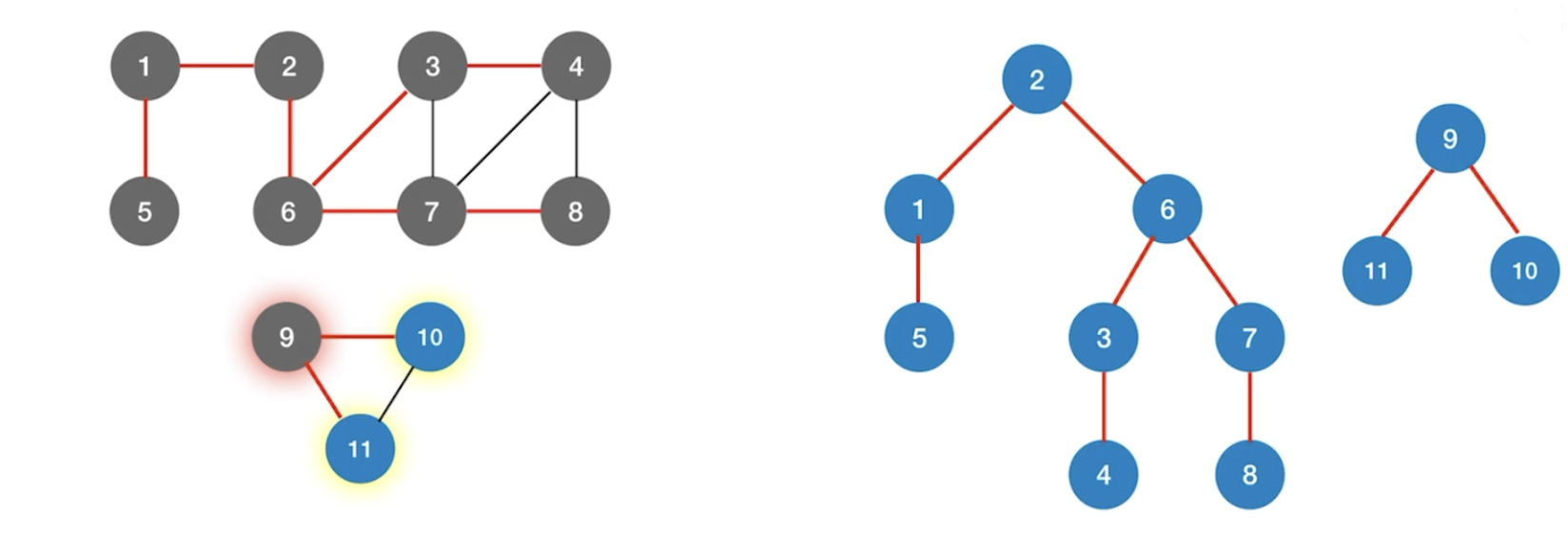
广度优先生成树
在广度优先遍历的过程中,我们可以得到一棵遍历树,称为广度优先生成树。需要注意的是,一给定图的邻接矩阵存储表示是唯一的,故其广度优先生成树也是唯一的,故其广度优先生成树也是不唯一的。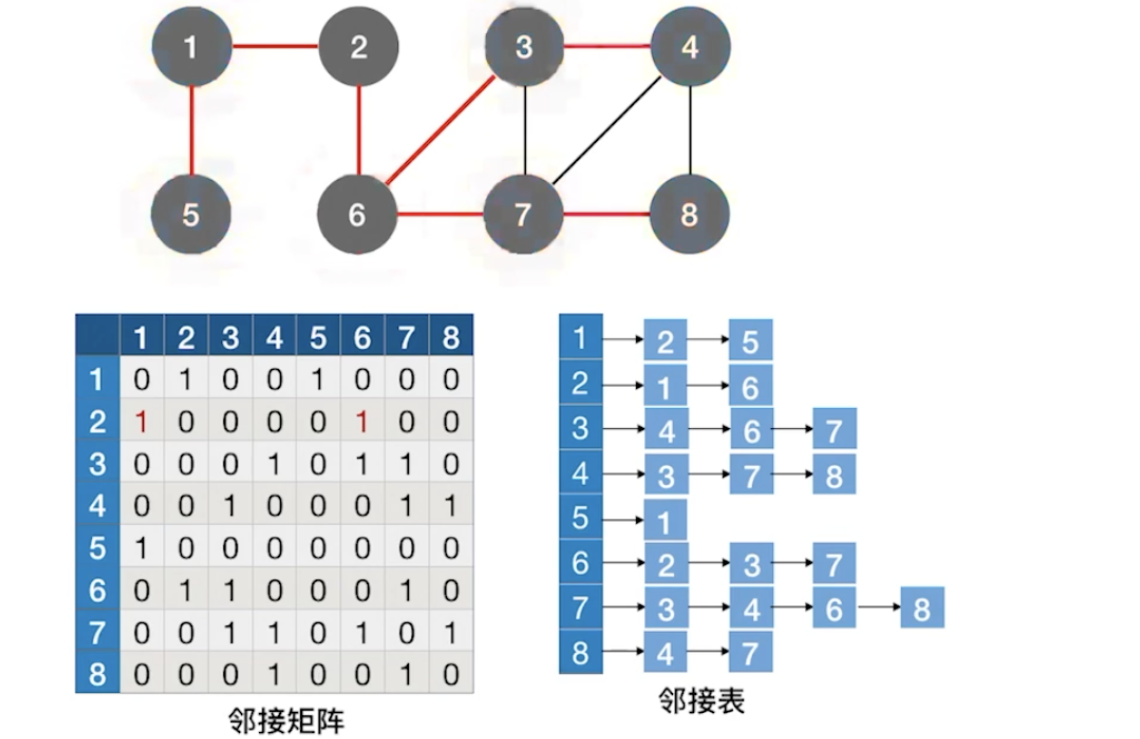
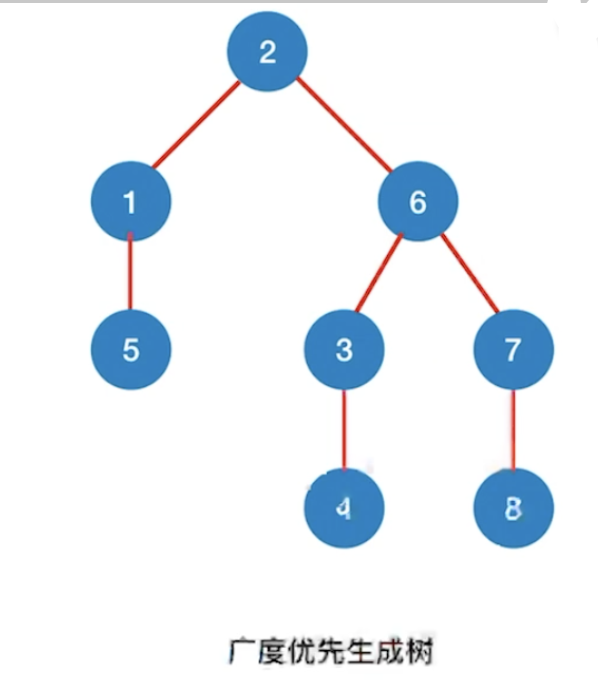
广度优先生成森林
对于非连通图的广度优先遍历,可以得到广度优先生成森林