(43)王道数据结构-十字链表和邻接多重表

十字链表

基本概念

十字链表是有向图的一种链式存储结构。在十字链表中，对应于有向图中的每条弧有一个结点，对应于每个顶点也有一个结点。

tailvex: 弧尾顶点编号
headvex: 弧头顶点编号
info: 权值
hlink: 弧头相同的下一条弧
tlink: 弧尾相同的下一条弧

弧结点中有5个域：尾域(tailvex)和头域(headvex)分别指示弧尾和弧头这两个顶点在图中的位置；链域hlink指向弧头相同的下一条弧；链域tlink指向弧尾相同的下一条弧；info域指向该弧的相关信息。这样，弧头相同的弧就在同一链表上，弧尾相同的弧也在同一个链表上。

data: 数据域
firstin: 该顶点作为弧头的第一条弧
firstout: 该顶点作为弧尾的第一条弧

顶点结点中有3个域：data域存放顶点相关的数据信息，如顶点名称；firstin和firstout两个域分别指向以该顶点为弧头或弧尾的第一个弧结点。

存储示例

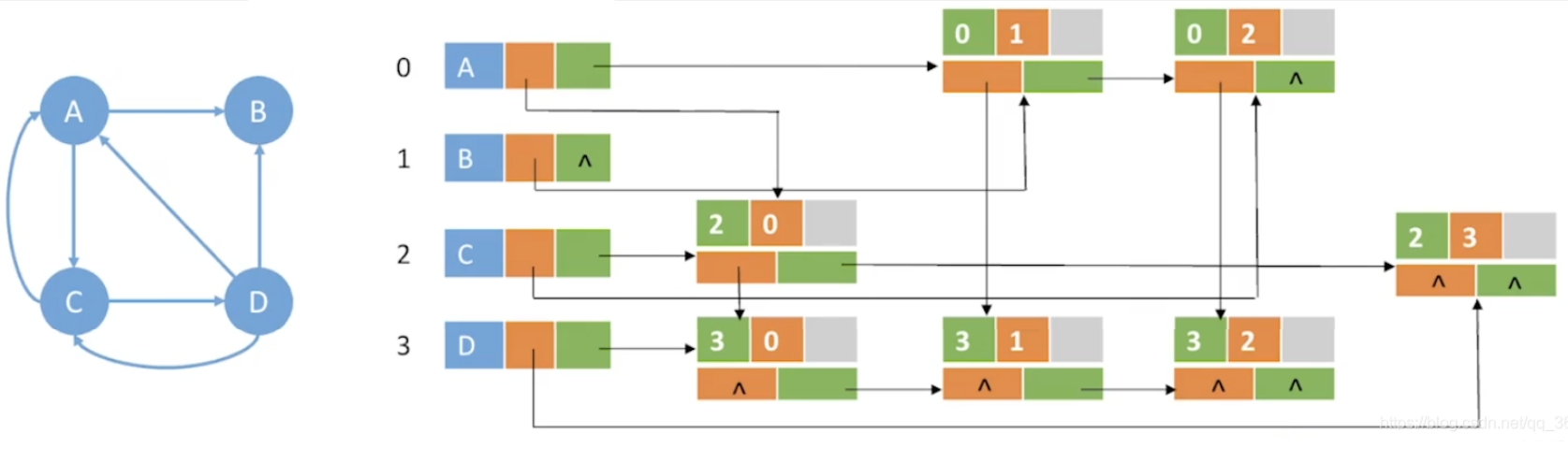
性能分析

在十字链表中，既容易找到vi为尾的弧，又容易找到vi为头的弧，因而容易求得顶点的出度和入度。图的十字链表表示是不唯一的，但一个十字链表表示确定一个图。

空间复杂度: O(|V| + |E|)
找指定顶点的所有出边: 顺着绿色线路找
找指定顶点的所有入边: 顺着橙色线路找
注意: 十字链表只能用于存储有向图

代码结构

//十字链表存储结构
#define MaxVertexNum 100 //图中顶点数目的最大值
typedef struct ArcNode{ //边表结点
    int tailvex, headvex; //该弧的头尾结点
    struct ArcNode *hlink, *tlink; //分别指向弧头相同和弧尾相同的结点
    //InfoType info; //相关信息指针
}ArcNode;

typedef struct VNode{ //顶点表结点
    VertexType data; //顶点信息
    ArcNode *firstin, *firstout; //指向第一条入弧和出弧
}VNode;

typedef struct{
    VNode xlist[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
}GLGraph; //GLGraph是以十字邻接存储的图类型

邻接多重表

存储优势

1.邻接表中每条边对应两份冗余信息，删除顶点、删除边等操作时间复杂度高
2.邻接矩阵法时间复杂度高

基本概念

邻接多重表是无向图的另一种链式存储结构。在邻接表中，容易求得顶点和边的各种信息，但在邻接表中求两个顶点之间是否存在边而对边执行删除等操作时，需要分别在两个顶点的边表中遍历，效率较低。

ivex,jvex: 边的两个顶点编号
info: 权值
ilink: 依附于顶点ivex的下一条边
jlink: 依附于顶点jvex的下一条边

其中，mark为标志域，可用以标记该条边是否被搜素过；ivex 和 jvex为该边依附的两个顶点在图中的位置；ilink指向下一条依附于顶点ivex的边；jlink指向下一条依附于顶点jvex的边，info为指向和边相关的各种信息的指针域。每个顶点也用一个结点表示

data: 数据域
firstedge: 与该顶点相连的第一条边

其中，data域存储该顶点的相关信息，firstedge域指示第一条依附于该顶点的边。在邻接多重表中，所有依附于同一顶点的边串联在同一链表中，由于每条边依附于两个顶点，因此每个边结点同时链接在两个链表中。

存储示例

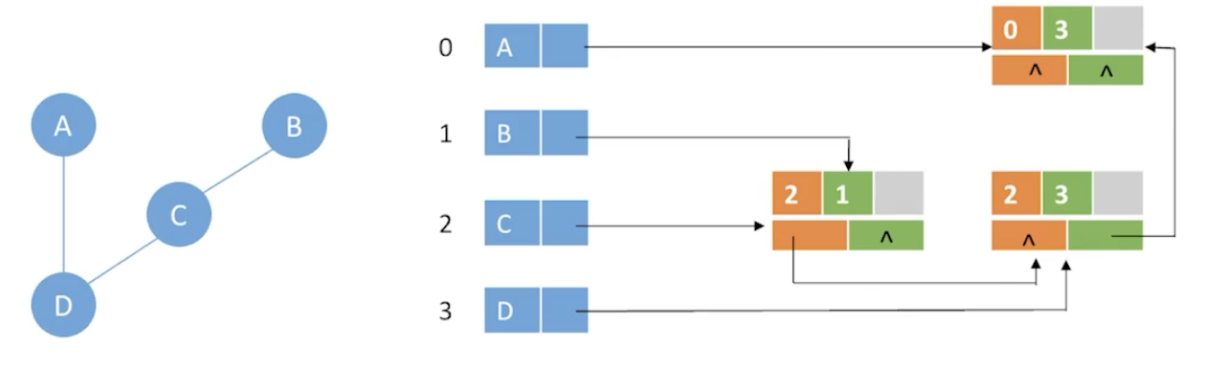
性能分析

空间复杂度: O(|V|+|E|) 每条边只对应一份数据
优点: 删除边、删除结点等操作很方便
注意:
1.邻接多重表只适用于存储无向图
2.每条边上只有一个结点

代码结构

#define MaxVertexNum 100 //图中顶点数目的最大值
typedef struct ArcNode{ //边表结点
    bool mark; //访问标记
    int ivex, jvex; //分别指向该弧的两个结点
    struct ArcNode *ilink, *jlink; //分别指向两个顶点的下一条边
    //InfoType info; //相关信息指针
}ArcNode;

typedef struct VNode{ //顶点表指针
    VertexType data; //顶点信息
    ArcNode *firstedge; //指向第一条依附该顶点的边
}VNode;

typedef struct{
    VNode adjmulist[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
}AMLGraph; //AMLGraph是以邻接多重表存储的图类型

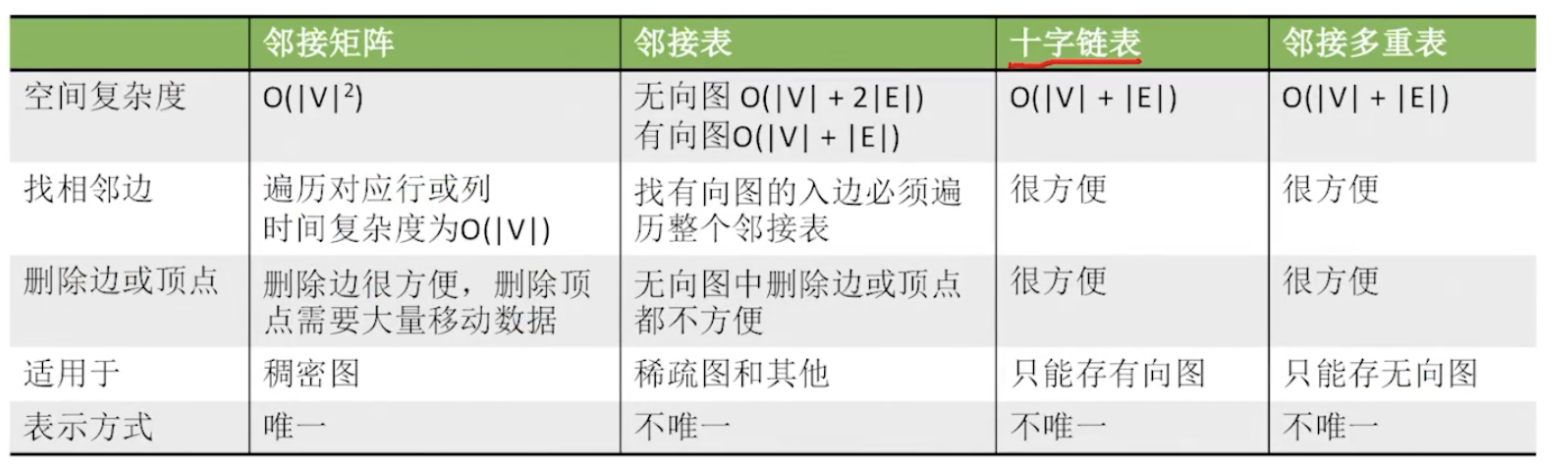
分类比较