(47)王道数据结构-最小生成树

基本概念

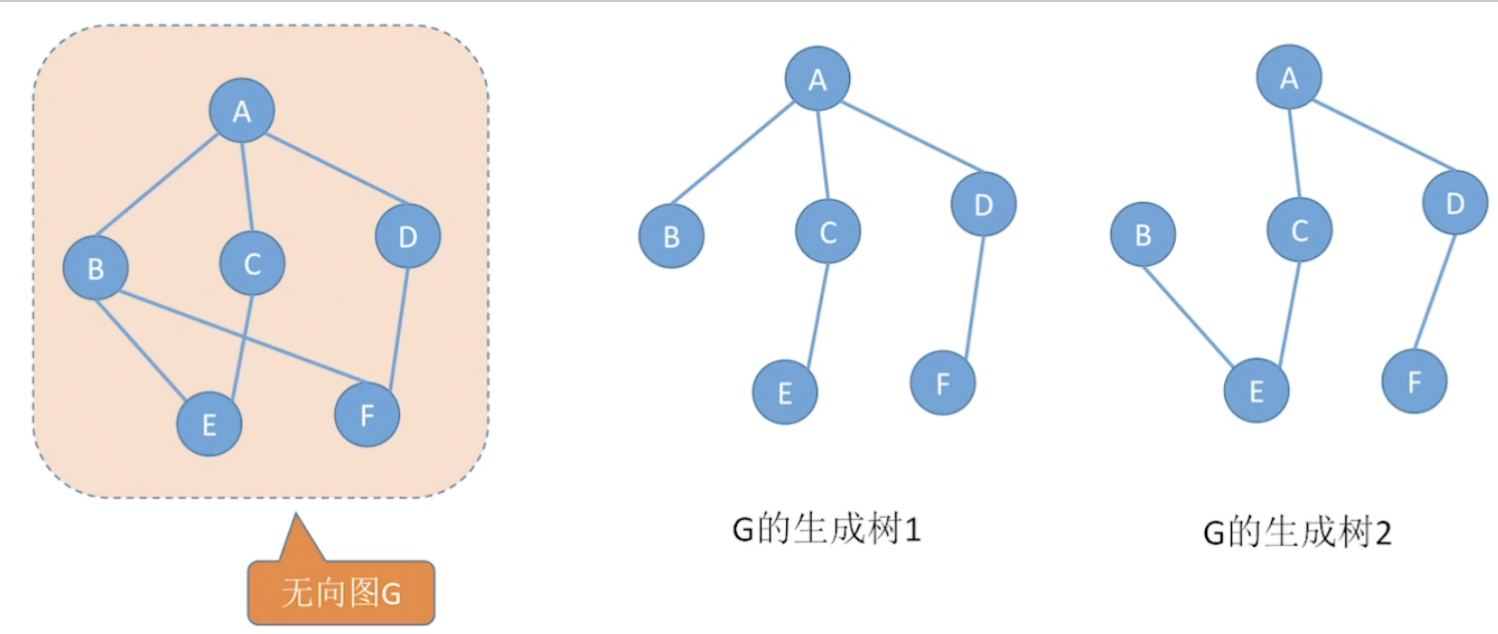
生成树

连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点树为n，则它的生成树含有n-1条边。对于生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会变成一个回路

最小生成树

最小生成树即最小代价树。一个连通图是生成树是图的极小连通子图，它包含图中的所有顶点，并且只含尽可能少的边。这意味着对于生成树来说，若砍去它的一条边，则会使生成树变成非连通图；若给它增加一条边，则会形成图中的一条回路。

对于一个带权连通无向图G=(V, E), 生成树不同，每棵树的权(即树中所有边上的权值之和可能不同。 设R为G的所有生成树的集合，若T为R中边的权值之和最小的那棵生成树，则T称为G的最小生成树(Minimum-Spanning Tee MST)。

重要性质

1)最小生成树不是唯一的，即最小生成树的树形不唯一，R中可能有多个最小生成树。当图 G中的各边权值互不相等时，G的最小生成树是唯一的；若无向连通图G的边数比顶点数少1，即G本身是一棵树时，则G的最小生成树就是它本身。

• 最小生成树可能有多个,但边的权值之和总是唯一且最小的
• 最小生成树的边数 = 顶点数 - 1。砍掉一条则不连通，增加一条则会出现回路

2)最小生成树的边的权值之和总是唯一的，虽然最小生成树不唯一，但其对应的边的权值之和总是唯一的，而且是最小的。

• 如果一个连通图本身就是一棵树，则其最小生成树就是它本身
• 只有连通图才有生成树，非联通图只有生成森林

3)最小生成树的边数为顶点数减1。

• 最小生成树可能有多个，但边的权值之和总是唯一且最小的
• 最小生成树的边数 = 顶点数 - 1。砍掉一条则不连通，增加一条边则会出现回路

构造算法

构造最小生成树有多种算法，但大多数算法都利用了最小生成树的下列性质：假设G=(V, E) 是一个带权连通无向图，U是顶点集V的一个非空子集。若(u, v)是一条具有最小权值的边，其中 u∈U, v∈V-U，则必存在一棵包含边(u, v)的最小生成树。

Prim算法(普里姆)

Prim (普里姆)算法的执行非常类似于寻找图的最短路径的Dijkstra算法。假设 N={V, E}是连通网，ET是N上最小生成树中边的集合。算法从VT= {u0} (u0∈V) ，ET= {}开始，重复执行下述操作：在所有u∈V，v∈V- VT的边(u, v)∈E中找一条代价最小的边(u0, v0)并入集合 ET，同时将v0并入VT，直至VT=V为止。此时E中必有n-1条边，则T= {VT, ET}为N的最小生成树。

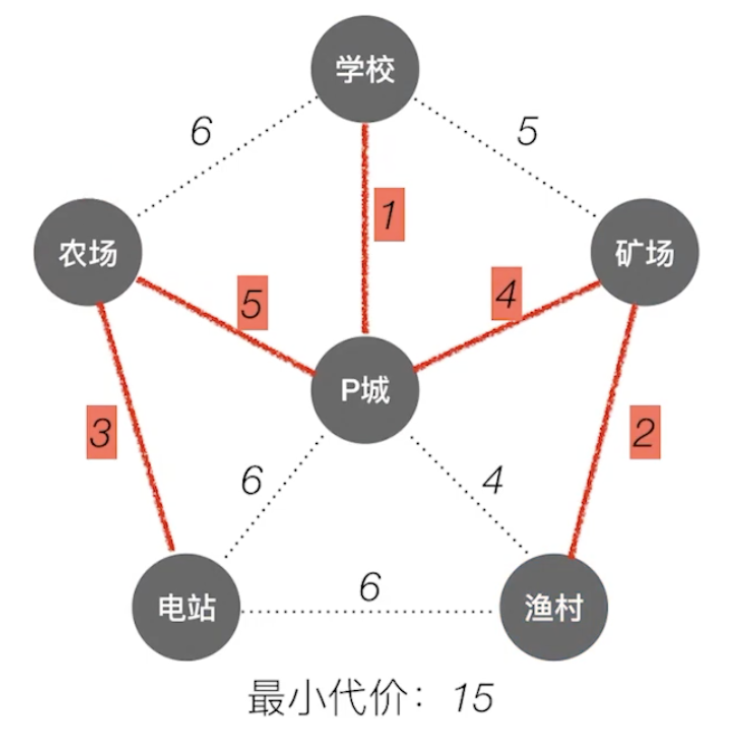
具体操作是从某一顶点开始构造生成树；每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。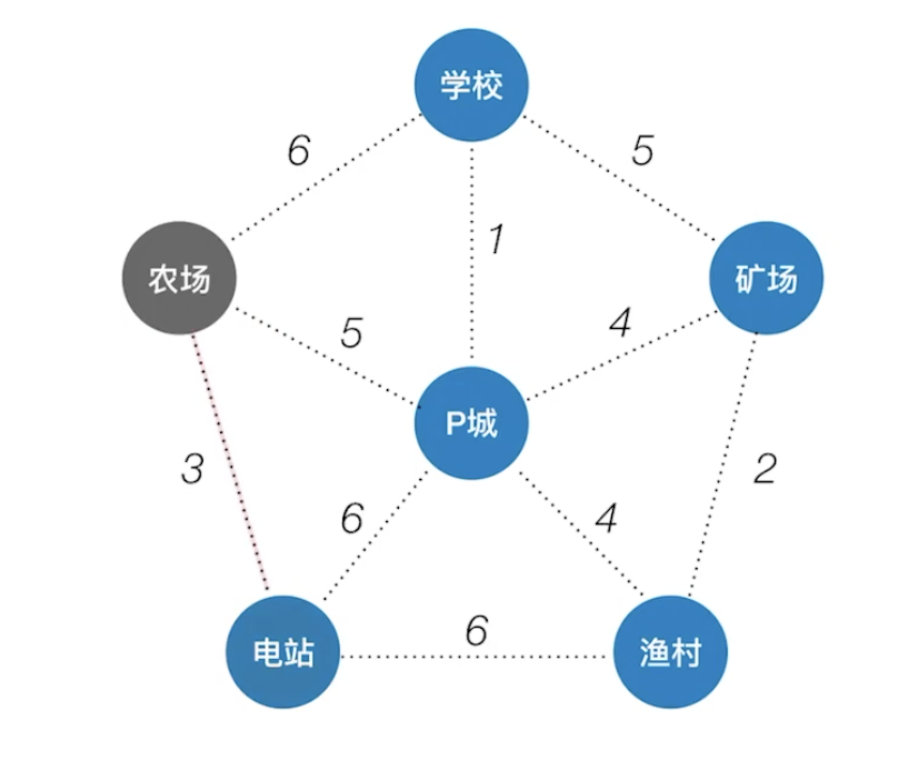

Kruskal算法(克鲁斯卡尔)

与Prim算法从顶点开始扩展最小生成树不同，Kruskal (克鲁斯卡尔)算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。假设N= (V, E)是连通网，对应的最小生成树T= (VT, ET)，Kruskal算法的步骤如下:

每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)直到所有结点都连通。在构造过程中，按照网中边的权值由小到大的顺序，不断选取当前未被选取的、边集中权值最小的边。依据生成树的概念，n个结点的生成树有n- 1条边，故反复上述过程，直到选取了n-1条边为止，这样就构成了一棵最小生成树。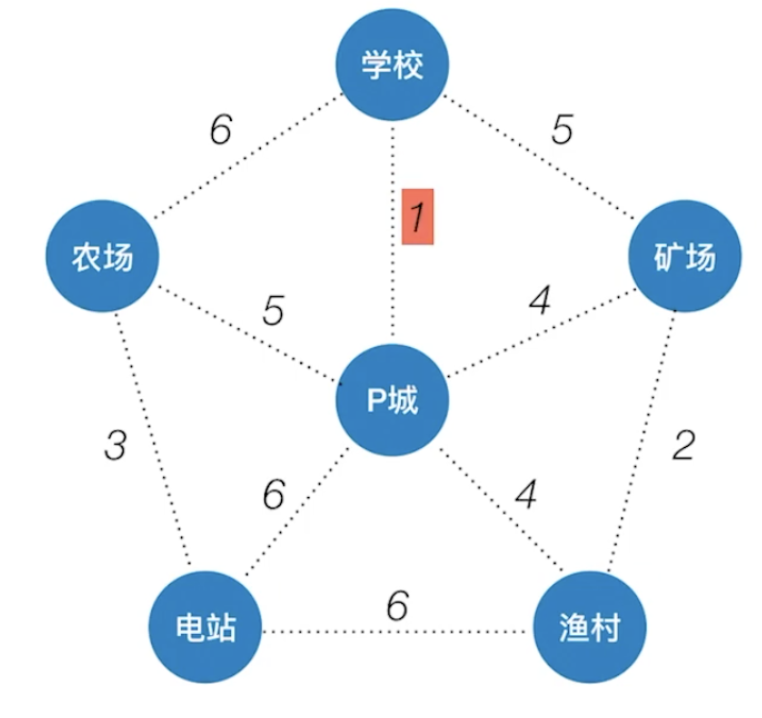

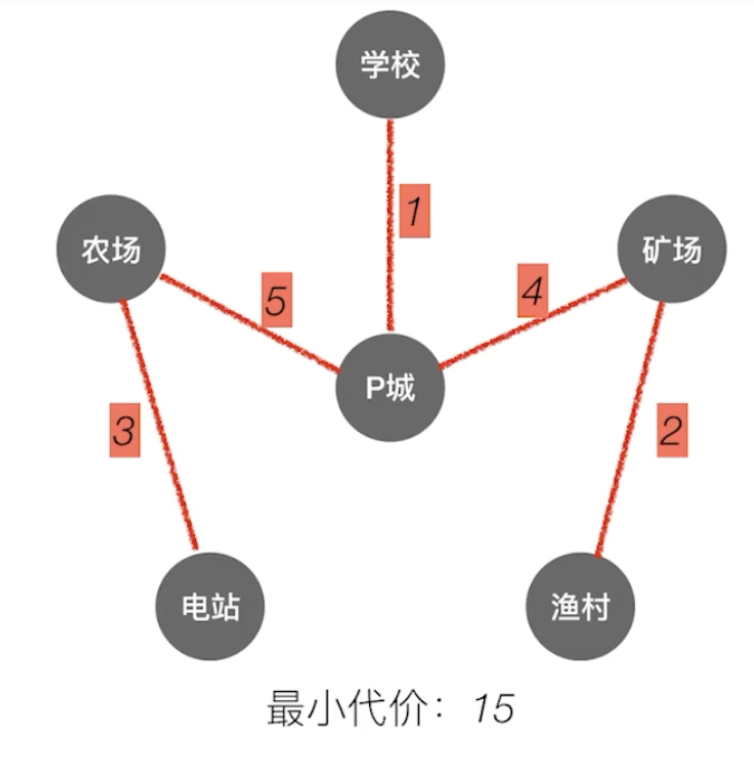
PK对比

构造方式

1.prim从某一顶点开始构造生成树；每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止
2.kruskal每次选择一条权值最小的边，使这两条连通(原本已经连通的就不选)

时间复杂度:
1.prim的时间复杂度O(|V|^2)适合用于边稠密图
2.kruskal的时间复杂度O(|E|log2|E|)适合用于边稀疏图

实现思想

prim

从v0开始，总共需要n-1轮处理

每一轮处理:循环遍历所有结点，找到lowCast最低的，且还没加入树的顶点

再次循环遍历，更新还没有加入的各个顶点的lowCase值

时间复杂度:
总时间复杂度O(n^2)即O(|V|^2)
每一轮时间复杂度O(2n)

代码逻辑

//Prim算法简单实现
void Prim(G,T) {
     T=∅; //初始化空树
     U={w}; //添加任一顶点w
     while((V-U)!=∅) {//若树中不含全部顶点
          设(u,v)是使u∈U与v∈(U-V)，且权值最小的边;
          T=T∪{(u,v)}; //边归入树
          U=U∪{v}; //顶点归入树
     }
}     

Prim 算法的时间复杂度为O(1)，不依赖于|E|，因此它适用于求解边稠密的图的最小生成树。虽然采用其他方法能改进Prim算法的时间复杂度，但增加了实现的复杂性。

kruskal

循环(重复下列操作至T是一棵树)：按G的边的权值递增顺序依次从E- ET 中选择一条边，若这条边加入T后不构成回路，则将其加入ET，否则舍弃，直到E中含有n-1条边。

代码逻辑

//Kruskal算法简单实现
void Kruskal(V,T) {
    T=V; //初始化树T，仅含顶点
    numS=n; //连通分量数
    while(numS>1) {//若连通分量数大于1
        从E中取出权值最小的边(v,u);
        if(v和u属于T中不同的连通分量) {
            T=T∪{(v,u)}; //将此边加入生成树中
            numS--; //连通分量数减1
        }
    }
}

若一条边连接了两棵不同树中的顶点，则对这两棵树来说，它必定是连通的，将这条边加入森林中，完成两棵树的合并，直到整个森林合并成一棵树。

通常在Kruskal算法中，采用堆来存放边的集合，因此每次选择最小权值的边只需O(log|E|)的时间。此外，由于生成树T中的所有边可视为一个等价类，因此每次添加新的边的过程类似于求解等价类的过程，由此可以采用并查集的数据结构来描述T，从而构造T的时间 复杂度为O(|E|log|E|)。因此，Kruskal 算法适合于边稀疏而顶点较多的图。