(46)王道数据结构-图的深度优先遍历

基本概念

深度优先搜索类似于树的先序遍历。首先访问图中某一起始顶点v，然后由v出发，访问与v邻接且未被访问的任一顶点w1，再访问与w1邻接且未被访问的任一顶点w2·····重复上述过程。当不能再继续向下访问时，依次退回到最近被访问的顶点，若它还有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直到图中所有顶点均被访问过为止。

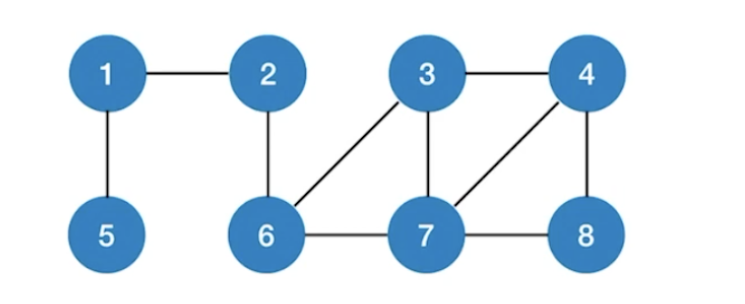
从2出发深度优先遍历序列: 2, 1, 5, 6, 3, 4, 7, 8

bool visited[MAX_VERTEX_NUM]; //访问标记数值
void DFS(Graph G, int v) {  //从顶点v出发，深度优先遍历图G
    visit(v); //访问顶点v
    visited[v] = TRUE; //设已访问标记
    for(w=FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)) {
        if(!visited[w]) { //w为u的尚未访问的邻接顶点  
            DFS(G, w);
        }
    } 
}

最终版(DFS)

解决了非联通图问题

bool visited[MAX_VERTEX_NUM]; //访问标记数值
void DFSTraverse(Graph G) {   //对图G进行深度优先遍历
    for(v=0; v<G.vexnum; ++v) {
        visited[v] = FALSE; //初始化已访问标记数据
    }  
    for(v=0; v<G.vexnum; ++v) {//本代码中从v=0开始遍历
        if(!visited[v]) {
            DFS(G, v);
        }  
    }
}
void DFS(Graph G, int v) {//从顶点v出发，深度优先遍历图G
    visit(v); //访问顶点v
    visited[v] = TRUE; //设已访问标记
    for(w=FirstNeighbor(G, v); w>=0; w=NextNeighor(G, v, w)) {
        if(!visited[w]) {//w为u的尚未访问的邻接顶点  
            DFS(G, w);
        }
    }  
}

1.图的邻接矩阵表示是唯一的，但对于邻接表来说，若边的输入次序不同，生成的邻接表也不同。
2.因此，对于同样一个图，基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的，基于邻接表的遍历所得到的DFS和BFS序列是不唯一的

复杂度分析

空间复杂度

DFS算法是一个递归算法，需要借助一个递归栈，故其空间复杂度为O(|V|)。其中函数调用栈道最坏情况，递归深度为O(|V|)
。最好情况时间复杂度为O(1)

时间复杂度

时间复杂度 = 访问各结点所需时间+探索各条边所需时间

1.用邻接矩阵表示，访问|V|个顶点需要O(|V|)的时间，查找每个顶点的邻接点都需要O(|V|)的时间，而总共有|V|个顶点，时间复杂度为O(|V|^2)

2.用邻接表表示，访问|V|个顶点需要O(|V|)的时间，查找各顶点的邻接点共需要O(|E|)的时间，时间复杂度=O(|V|+|E|)

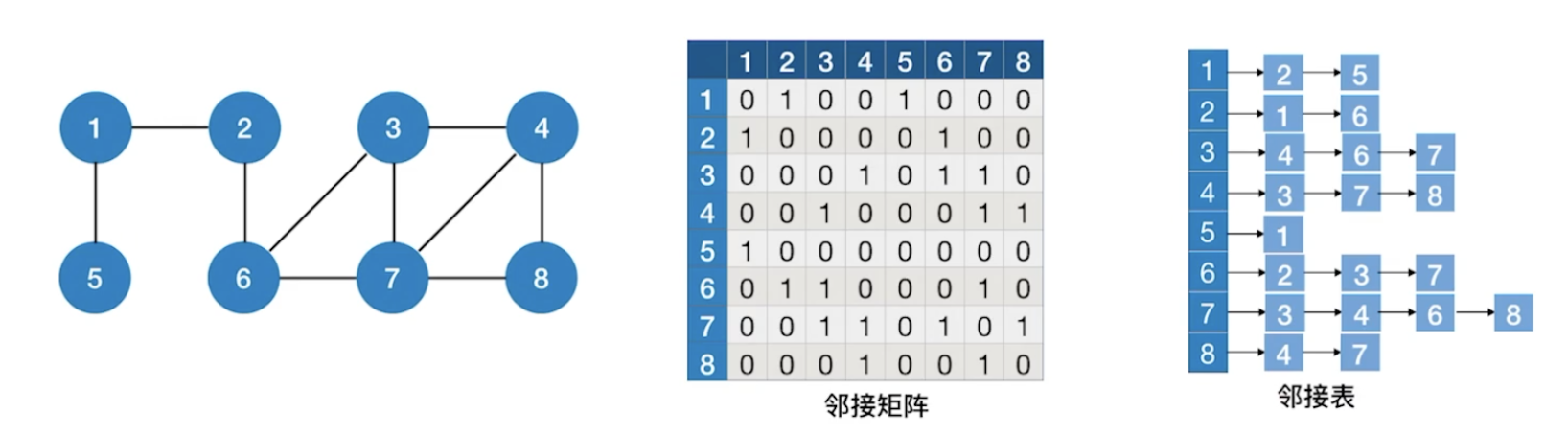
从2出发的深度优先遍历序列: 2, 1, 5, 6, 3, 4, 7, 8
从3出发的深度优先遍历序列: 3, 4, 7, 6, 2, 1, 5, 8
从1出发的深度优先遍历序列: 1, 2, 6, 3, 4, 7, 8, 4

深度优先生成树

对连通图调用DFS才能深度优先生成树，否则产生的将是深度优先生成森林。

1.同一个图的邻接矩阵表示方式唯一，因此深度优先遍历序列唯一，深度优先生成树也唯一
2.同一个图邻接表表示方式不唯一，因此深度优先遍历序列不唯一，深度优先生成树也唯一


graph TD;
    A(("1"));
    B(("2"));
    C(("3"));
    D(("4"));
    E(("5"));
    F(("6"));
    G(("7"));
    H(("8"));
    
    B-->A;
    B-->F;
    A-->E;

    F-->C;
    C-->D;
    D-->G;
    G-->H;

生成森林


graph TD;
    A(("1"));
    B(("2"));
    C(("3"));
    D(("4"));
    E(("5"));
    F(("6"));
    G(("7"));
    H(("8"));
    I(("I"));
    J(("J"));
    K(("K"));
    
    B-->A;
    B-->F;
    A-->E;

    F-->C;
    C-->D;
    D-->G;
    G-->H;

    I-->J;
    J-->K;