(58)王道数据结构-B树
原文地址:B树
基本概念
B树(Balance Tree),它是专门为磁盘数据读取设计的一种度为 m 的查找树(多用于数据库)它同样是一棵平衡树,但是不仅限于二叉。得益于B树这种结点少,高度平衡且有序的性质,而硬盘IO速冻远低于内存,我们希望能够花费尽可能少的时间找到我们想要的数据,减少IO次数,B树就非常适合在硬盘上的保存数据,它的查找效率是非常高的。
基本规则
1.树中每个结点最多含有m个孩子(m >= 2)比如上面就是m为4的4阶B树,最多有4个孩子
2.除根结点和叶子结点外,其它每个结点至少有⌈m/2⌉个孩子,同理键值数量至少有⌈m/2⌉-1个
3.若根结点不是叶子结点,则至少有2个孩子
4.所有叶子结点都出现在同一层
5.一个结点的包含多种信息(P0,K1,P1,K2,…,Kn,Pn),其中P为指向子树的指针,K为键值(关键字)
Ki (i=1…n)为键值,也就是每个结点保存的值,且键值按顺序升序排序K(i-1)< Ki
Pi为指向子树的指针,且指针Pi指向的子树中所有结点的键值均小于Ki,但都大于K(i-1)
键值的个数n必须满足: ⌈m/2⌉-1 <= n <= m-1
在线动画网站:https://www.cs.usfca.edu/~galles/visualization/BTree.html
操作步骤
例子中用的是度为3的B树
插入操作
第一步:
树中节点:1
插入1之后,只有一个结点
第二步:
树中节点:1,2
满足规则:如果该节点上的元素数未满,则将新元素插入到该节点,并保持节点中元素的顺序
第三步: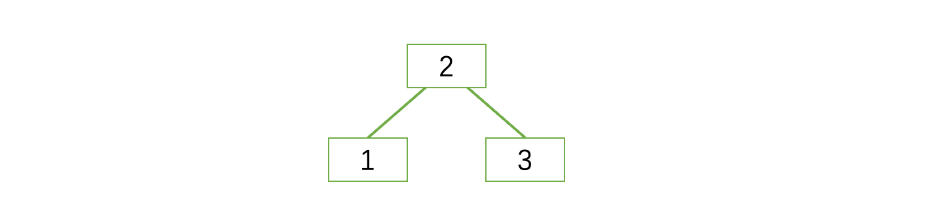
之后插入一个3进去,但是此时因为3,那么键值最多只能有两个,肯定是装不下的,此时满足以下规则
- 如果该节点上的元素已满,则需要将该节点平均地分裂成两个节点
- 小于中位数的元素作为左子树划分出去,大于中位数的元素作为右子树划分
- 分割值此时上升到父节点中,如果没有父节点,那么就创建一个新的
第四步: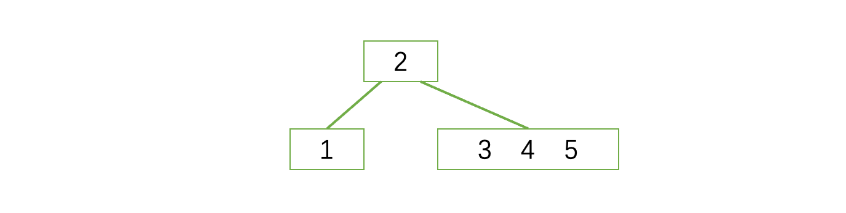
需要注意的是,插入按照小的走左边,大的走右边的原则
第五步: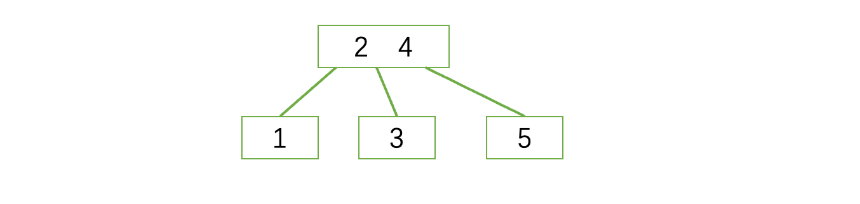
1.首先3、4、5三个都分开,其中4作为分割值
2.3、5变成两个独立的数,此时4上升到父节点,所以到上面去了
3.3、5出现在4的左右两边
4.这里不是向下划分,需要满足所有叶子结点都出现同一层
第六步: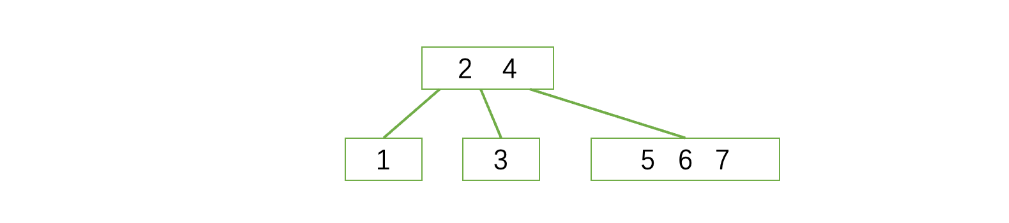
继续插入6、7
第七步: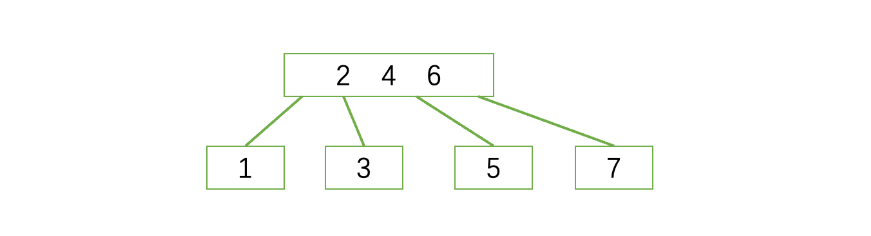
按照之前的操作,对右下角进行分裂,但新的分割结值上升之后最上面的结点挤爆
最后一步: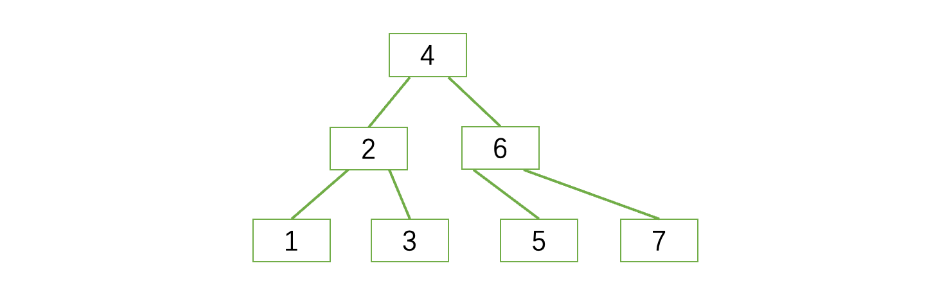
在2、4、6中寻找一个新的分割值,分裂后将其上升到新的父节点中
删除操作
以一棵5阶B树为例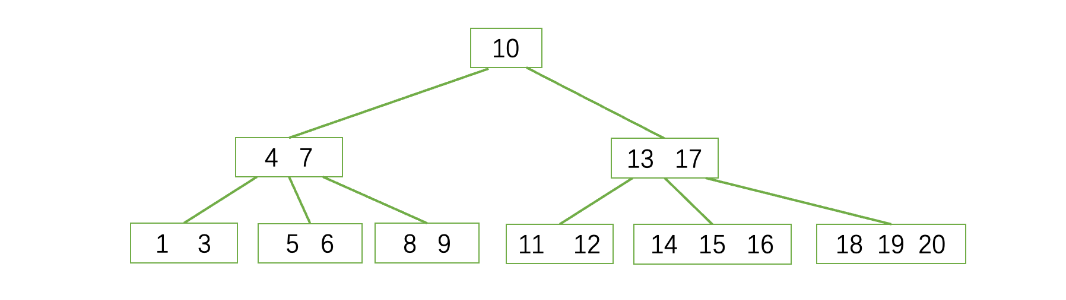
删除’16’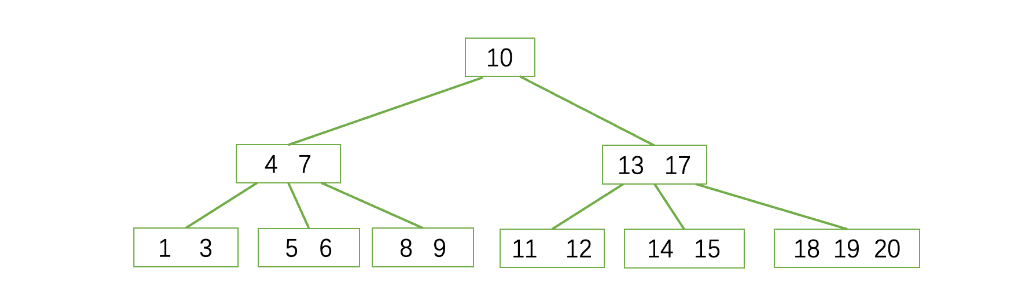
删除后,依旧满足B树的性质,所以无需其他操作
删除’15’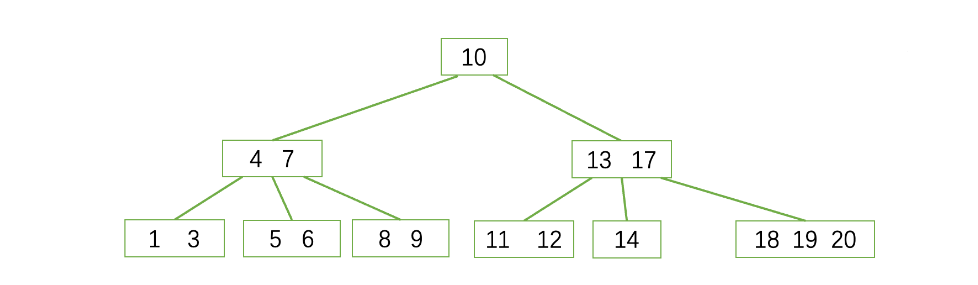
1.删除后,节点中只有14,不满足B树的性质
2.除了根结点和叶子结点外,其他结点至少有[m/2]个孩子,同理键值数量至少有[m/2]-1个,现在只有一个是不行的
3.需要向兄弟借一个(只能找左右两边的兄弟)
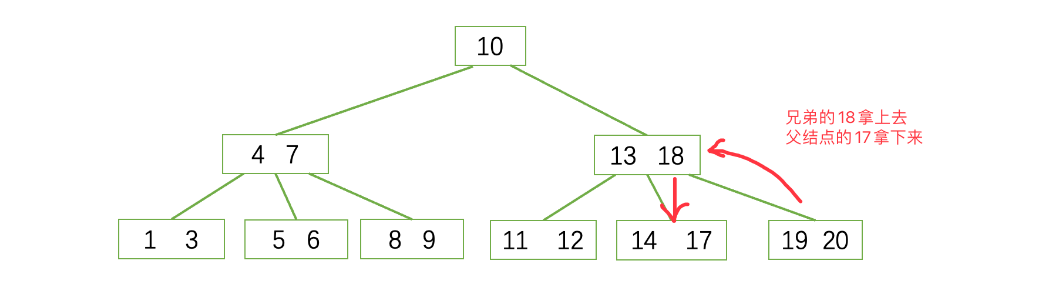
删除’17’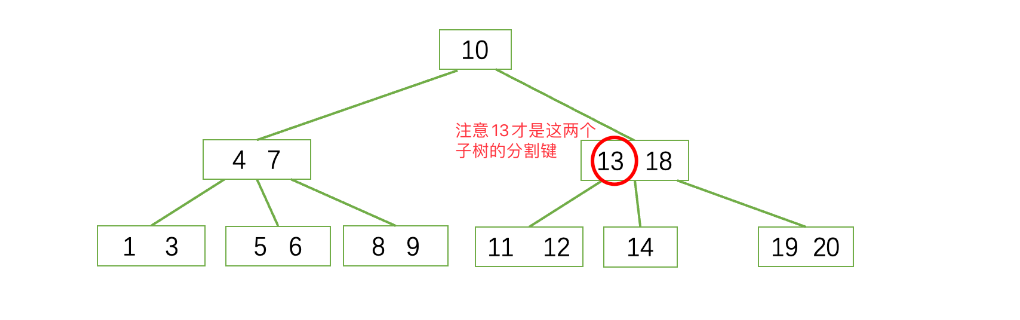
删除17后,兄弟节点已经没有办法借元素了。只能合并兄弟节点和与分割键
合并后存在:
1.父节点只有一个元素
2.兄弟节点也无法借
3.只能继续合并
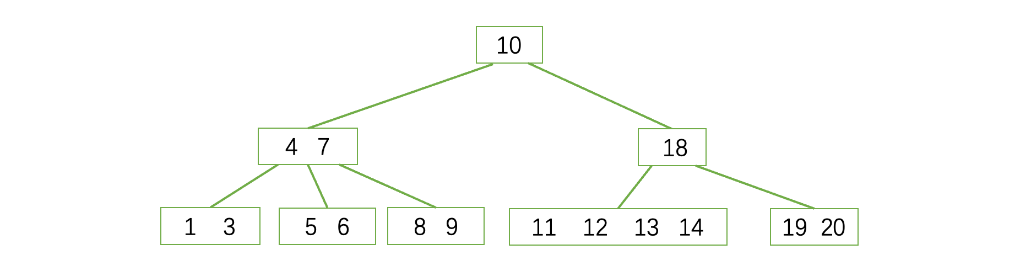
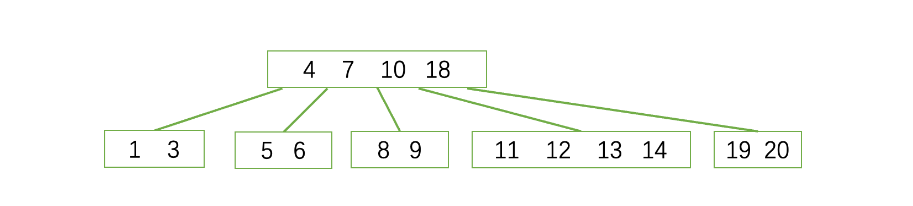
合并后的树
删除’4’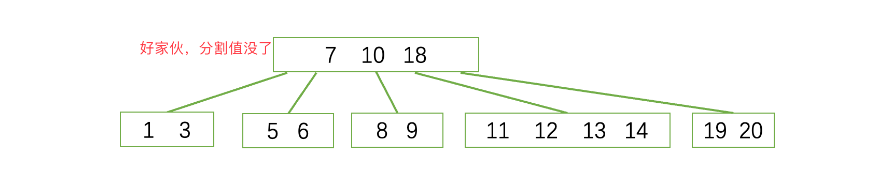
会导致失去分割值,需要继续寻找分割值,选取左边最大的作为分割值

1.左边结点不满足性质,元素数量低于限制
2.找兄弟借,兄弟无法借
3.只能合并兄弟
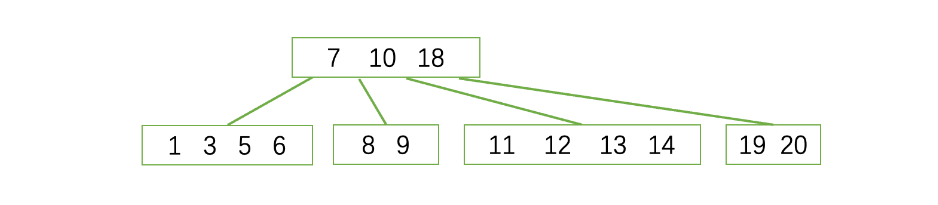
合并完成,整个变换过程中,这颗B树所有子树的高度是一直维持在一个稳定状态的,查找效率可以保持
删除总结
●若删除的是叶子结点的中元素:
正常情况下直接删除。
如果删除后,键值数小于最小值,那么需要找兄弟借一个。
要是没得借了,直接跟兄弟结点、对应的分割值合并。
●若删除的是某个根结点中的元素:
一般情况会删掉一个分割值,删掉后需要重新从左右子树中找一个新分割值的拿上来。
要是拿上来之后左右子树中出现键值数小于最小值的情况,那么就只能合并了。
●上述两个操作执行完后,还要继续往上看上面的结点是否依然满足性质,否则继续处理,直到稳定。